题目内容
下列函数中，在定义域内既是偶函数又在（0，+∞）上单调递增的是（ ）
| A、y=x3 |
| B、y=3x |
| C、y=cosx |
| D、y=ln|x| |
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：根据函数的奇偶性和单调性的定义和性质分别判断每个函数的奇偶性和单调性即可．
解答：
解：A．函数y=x3为奇函数，在（0，+∞）上单调递增，所以A不合适．
B．y=3x是非奇非偶函数，所以B不合适．
C，函数y=cosx为偶数，但在（0，+∞）上不单调，所以C不合适．
D．函数y=ln|x|为偶函数，在（0，+∞）上单调递增，所以D合适．
故选D．
B．y=3x是非奇非偶函数，所以B不合适．
C，函数y=cosx为偶数，但在（0，+∞）上不单调，所以C不合适．
D．函数y=ln|x|为偶函数，在（0，+∞）上单调递增，所以D合适．
故选D．
点评：本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见基本函数的奇偶性和单调性．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
设tanα、tanβ是方程x2+x-2=0的两实数根，则tan（α+β）的值为（ ）
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知α是第二象限角，P（x，
）为其终边上一点，且cosα=
x，则x=（ ）
| 5 |
| ||
| 4 |
A、
| ||
B、±
| ||
C、-
| ||
D、-
|
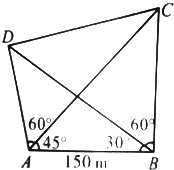如图，A、B、C、D是河两岸的四根电线杆，A、B在河这边，C、D在河对岸，现在距离A处150m的B处测得∠ABD=30°，∠DBC=60°，而在A处测得∠BAC=45°，∠CAD=60°，求C、D两点间的距离．（已知A、B、C、D在同一平面内）．在“由于任何数的平方都是非负数，所以（2i）2≥0”这一推理中，产生错误的原因是（ ）
| A、推理的形式不符合三段论的要求 |
| B、大前提错误 |
| C、小前提错误 |
| D、推理的结果错误 |