Question

已知数列{an}中，a1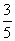＝，an＝2－(n≥2，n∈N*)，数列{bn}满足bn＝(n∈N*)．

(1)证明：数列{bn}是等差数列；

(2)若Sn＝(a1－1)·(a2－1)＋(a2－1)·(a3－1)＋…＋(an－1)·(an＋1－1)，是否存在a，b∈Z，使得a≤Sn≤b恒成立？若存在，求出a的最大值与b的最小值；若不存在，请说明理由．

Answer 1

解　(1)由题意，知当n≥2时，

所以bn－bn－1＝＝1(n∈N*，n≥2)．

所以{bn}是首项为b1＝＝－，公差为1的等差数列．

(2)由(1)，知bn＝n－.依题意，有Sn＝(a1－1)·(a2－1)＋(a2－1)·(a3－1)＋…＋(an－1)·(an＋1－1)＝·＋·＋…＋·＝－＝－－

设函数y＝，当x>时，y>0，y′<0，则函数在上为减函数，

故当n＝3时，Sn＝－－取最小值－.

而函数y＝在x<时，y<0，

上也为减函数，

故当n＝2时，Sn取得最大值.

故a的最大值为－3，b的最小值为2.