题目内容
已知q和n均为给定的大于1的自然数.设集合M={0,1,2,…,q-1},集合A={x|x=x1+x2q+…+xnqn-1,xi∈M,i=1,2,…,n}.
(1)当q=2,n=3时,用列举法表示集合A;
(2)设s,t∈A,s=a1+a2q+…+anqn-1,t=b1+b2q+…+bnqn-1,其中ai,bi∈M,i=1,2,…,n.证明:若an<bn,则s<t.
解 (1)当q=2,n=3时,M={0,1},A={x|x=x1+x2·2+x3·22,xi∈M,i=1,2,3}.
可得,A={0,1,2,3,4,5,6,7}.
(2)证明:由s,t∈A,s=a1+a2q+…+anqn-1,t=b1+b2q+…+bnqn-1,ai,bi∈M,i=1,2,…,n及an<bn,
可得s-t=(a1-b1)+(a2-b2)q+…+(an-1-bn-1)qn-2+(an-bn)qn-1≤(q-1)+(q-1)q+…+(q-1)qn-2-qn-1
= -qn-1=-1<0.
-qn-1=-1<0.
所以,s<t.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 B.4
B.4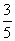 ,an=2-
,an=2- (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).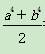 ≤0
≤0 -1-a2b2≤0
-1-a2b2≤0 的图象上的点,Bn(n,bn)为函数y=x图象上的点,其中n∈N*,设cn=an-bn,则cn与cn+1的大小关系为__________.
的图象上的点,Bn(n,bn)为函数y=x图象上的点,其中n∈N*,设cn=an-bn,则cn与cn+1的大小关系为__________.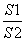 =
=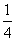 ,推广到空间可以得到类似结论:已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论:已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则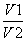 =( )
=( )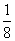 B.
B.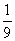
 D.
D.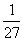
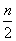 个
个 个
个 表示的平面区域,并回答下列问题:
表示的平面区域,并回答下列问题: