题目内容
若函数f（x）=
，x∈（a，1）是非奇非偶函数，则实数a的取值范围是 ．
| 1-3x |
| 1+3x |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：先验证函数是否满足f（-x）=-f（x），再看定义域是否关于原点对称，如果一个函数的定义域不关于原点对称，此函数就是非奇非偶函数．
解答：
解：∵f(-x)=
=
=-f(x)，
∴只要函数f（x）的定义域关于原点对称，则函数f（x）就是奇函数，
∴a≠-1，
故答案为：（-∞，-1）∪（-1，+∞）
| 1-3-x |
| 1+3-x |
| 3x-1 |
| 3x+1 |
∴只要函数f（x）的定义域关于原点对称，则函数f（x）就是奇函数，
∴a≠-1，
故答案为：（-∞，-1）∪（-1，+∞）
点评：本题主要考查函数奇偶性的定义，函数是奇偶函数的必要条件是定义域要关于原点对称，属于低档题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
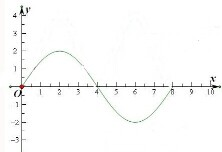已知函数f（x）=Asinωx（A＞0，ω＜0）的部分图象如图所示，则函数f（x）是（ ）| A、周期为8的偶函数 |
| B、周期为8的奇函数 |
| C、周期为8π的偶函数 |
| D、周期为8π的奇函数 |