题目内容
已知定义在R上的函数f（x），满足f（1+x）=f（1-x），f（x）=f（4-x）．且当x∈[-1，1]时，f（x）=ex，则f（2013）= ．
考点：抽象函数及其应用,函数的值
专题：函数的性质及应用
分析：根据f（1+x）=f（1-x），f（x）=f（4-x）得到函数f（x）是以2为周期的周期函数，继而得到f（2013）=f（1006×2+1）=f（1），问题得以解决．
解答：
解：∵f（1+x）=f（1-x），
令x=x-1，
则f（x）=f（2-x），
∵f（x）=f（4-x），
∴f（2-x）=f（4-x），
∴f（x）=f（x+2），
∴函数f（x）是以2为周期的周期函数，
∵2013=1006+1，
∴f（2013）=f（1006×2+1）=f（1），
∵当x∈[-1，1]时，f（x）=ex，
∴f（2013）=f（1）=e
故答案为：e
令x=x-1，
则f（x）=f（2-x），
∵f（x）=f（4-x），
∴f（2-x）=f（4-x），
∴f（x）=f（x+2），
∴函数f（x）是以2为周期的周期函数，
∵2013=1006+1，
∴f（2013）=f（1006×2+1）=f（1），
∵当x∈[-1，1]时，f（x）=ex，
∴f（2013）=f（1）=e
故答案为：e
点评：本题主要考查了抽象函数的问题，关键是求出函数为周期函数，属于中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
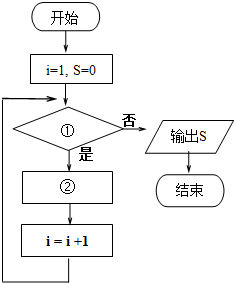已知等比数列{an}中，a1=1，公比q=2，计算数列{an}的前20项的和S，现已给出该算法的程序框图如图所示：