题目内容
1.已知f(x)=|x-1|+|x+a|,g(a)=a2-a-2.(1)当a=3,解关于x的不等式f(x)>g(a)+2;
(2)当x∈[-a,1)时恒有f(x)≤g(a),求实数a的取值范围.
分析 (1)若a=3,f(x)=|x-1|+|x+3|,g(3)=4,f(x)>g(a)+2化为|x-1|+|x+3|>6,即可得出结论;
(2)当x∈[-a,1]时恒有f(x)≤g(a),1+a≤a2-a-2,即可求实数a的取值范围.
解答 解:(1)a=3时,f(x)=|x-1|+|x+3|,g(3)=4,
f(x)>g(a)+2化为|x-1|+|x+3|>6,
x<-3时,-x+1-x-3>6,∴x<-4,
-3≤x≤1时,-x+1+x+3>6,无解,
x>1时,x-1+x+3>6,∴x>2.
综上所述,x<-4或x>2,
∴不等式的解集为{x|x<-4或x>2};
(2)∵x∈[-a,1],∴f(x)=1+a,
∴f(x)≤g(a),化为1+a≤a2-a-2,
∴a2-2a-3≥0,
∴a≥3或a≤-1,
又-a<1,∴a>-1,
∴a≥3.
点评 本题考查绝对值不等式的解法,考查恒成立问题,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
11.已知集合A={x|y=$\sqrt{1-x}$},B={y|y=2x+lna},且A⊆∁RB,则实数a的取值范围是( )
| A. | [e,+∞) | B. | (0,e] | C. | (-∞,1] | D. | (0,1] |
12.已知直线l1与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)交于A,B两点,且AB中点M的横坐标为b,过M且与直线l1垂直的直线l2过双曲线C的右焦点,则双曲线的离心率为( )
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | C. | $\frac{1+\sqrt{3}}{2}$ | D. | $\sqrt{\frac{1+\sqrt{3}}{2}}$ |
16.△ABC的内角A、B、C的对边分别为a、b、c.已知a=3,$c=\sqrt{2}$,$cosA=-\frac{{\sqrt{10}}}{10}$,则b=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | 2 | D. | 3 |
13.若x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{y≥1}\end{array}\right.$,则z=y+2x的最小值为( )
| A. | -1 | B. | 7 | C. | 2 | D. | 5 |
6.设点A(2,0),B(0,4),O(0,0),则△AOB的外接圆的方程为( )
| A. | x2+y2-2x+4y=0 | B. | x2+y2-2x+2y=0 | C. | x2+y2-2x-4y=0 | D. | x2+y2-2x-2y=0 |
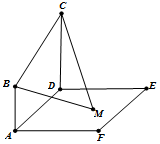 已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.
已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.