题目内容
13.若x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{y≥1}\end{array}\right.$,则z=y+2x的最小值为( )| A. | -1 | B. | 7 | C. | 2 | D. | 5 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{y≥1}\end{array}\right.$作出可行域,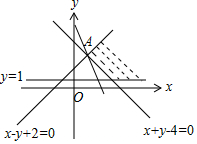
联立$\left\{\begin{array}{l}{x-y+2=0}\\{x+y-4=0}\end{array}\right.$,解得A(1,3).
化目标函数z=y+2x为y=-2x+z,由图可知,当直线y=-2x+z过A时,直线在y轴上的截距最小,z有最小值为5.
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
5.已知α为锐角,且$sinα=\frac{4}{5}$,则cos(π-α)=( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
2.已知抛物线y2=4x的焦点F与椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的一个焦点重合,它们在第一象限内的交点为P,且PF与x轴垂直,则椭圆的离心率为( )
| A. | $\sqrt{3}-\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
18.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+({a+1})x+2a,({x>0})\\{log_a}({x+1})+1,({-1<x≤0})\end{array}\right.$,(a<0,a≠1),若函数y=|f(x)|在$[{-\frac{1}{3},+∞})$上单调递增,且关于x的方程|f(x)|=x+3恰有两个不同的实根,则a的取值范围为( )
| A. | $[{\frac{3}{2},2})$ | B. | $({1,\frac{3}{2}}]∪\left\{{2,6}\right\}$ | C. | {2,6} | D. | $[{\frac{3}{2},\frac{5}{3}}]$ |