题目内容
20. 如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
分析 (1)运用线面垂直的判定定理可得PA⊥平面ABC,再由性质定理即可得证;
(2)要证平面BDE⊥平面PAC,可证BD⊥平面PAC,由(1)运用面面垂直的判定定理可得平面PAC⊥平面ABC,再由等腰三角形的性质可得BD⊥AC,运用面面垂直的性质定理,即可得证;
(3)由线面平行的性质定理可得PA∥DE,运用中位线定理,可得DE的长,以及DE⊥平面ABC,求得三角形BCD的面积,运用三棱锥的体积公式计算即可得到所求值.
解答 解:(1)证明:由PA⊥AB,PA⊥BC,
AB?平面ABC,BC?平面ABC,且AB∩BC=B,
可得PA⊥平面ABC,
由BD?平面ABC,
可得PA⊥BD;
(2)证明:由AB=BC,D为线段AC的中点,
可得BD⊥AC,
由PA⊥平面ABC,PA?平面PAC,
可得平面PAC⊥平面ABC,
又平面ABC∩平面ABC=AC,
BD?平面ABC,且BD⊥AC,
即有BD⊥平面PAC,
BD?平面BDE,
可得平面BDE⊥平面PAC;
(3)PA∥平面BDE,PA?平面PAC,
且平面PAC∩平面BDE=DE,
可得PA∥DE,
又D为AC的中点,
可得E为PC的中点,且DE=$\frac{1}{2}$PA=1,
由PA⊥平面ABC,
可得DE⊥平面ABC,
可得S△BDC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×2×2=1,
则三棱锥E-BCD的体积为$\frac{1}{3}$DE•S△BDC=$\frac{1}{3}$×1×1=$\frac{1}{3}$.
点评 本题考查空间的线线、线面和面面的位置关系的判断,主要是平行和垂直的关系,注意运用线面平行的性质定理以及线面垂直的判定定理和性质定理,面面垂直的判定定理和性质定理,同时考查三棱锥的体积的求法,考查空间想象能力和推理能力,属于中档题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
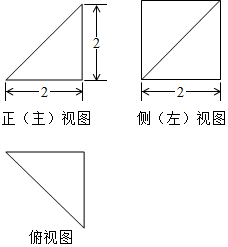
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |

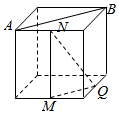
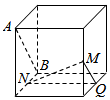
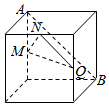
 如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.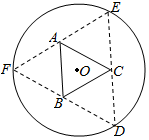 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.
如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.