题目内容
2.(x+y)(2x-y)5的展开式中的x3y3系数为 ( )| A. | -80 | B. | -40 | C. | 40 | D. | 80 |
分析 (2x-y)5的展开式的通项公式:Tr+1=${∁}_{5}^{r}$(2x)5-r(-y)r=25-r(-1)r${∁}_{5}^{r}$x5-ryr.令5-r=2,r=3,解得r=3.令5-r=3,r=2,解得r=2.即可得出.
解答 解:(2x-y)5的展开式的通项公式:Tr+1=${∁}_{5}^{r}$(2x)5-r(-y)r=25-r(-1)r${∁}_{5}^{r}$x5-ryr.
令5-r=2,r=3,解得r=3.
令5-r=3,r=2,解得r=2.
∴(x+y)(2x-y)5的展开式中的x3y3系数=22×(-1)3${∁}_{5}^{3}$+23×$1×{∁}_{5}^{2}$=40.
故选:C.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则C的离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
12.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
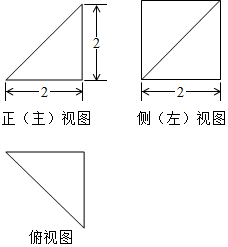

| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |

 如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.