题目内容

5．“x2+2x-8＞0”是“x＞2”成立的（　　）
A．必要不充分条件B．充分不必要条件
C．充要条件D．既不充分也不必要条件

分析 解不等式，根据充分必要条件的定义结合集合的包含关系判断即可．

解答 解：由x2+2x-8＞0，解得：x＞2或x＜-4，
故“x2+2x-8＞0”是“x＞2”成立的必要不充分条件，
故选：A．

点评 本题考查了充分必要条件，考查集合的包含关系，是一道基础题．

练习册系列答案
相关题目
15．已知等比数列{an}的各项均为正数，Sn为其前n项和，对于任意的n∈N*，满足关系式2Sn=3an-3．
（1）求数列{an}的通项公式；
（2）设数列{bn}的通项公式是bn=$\frac{1}{lo{g}_{3}{a}_{n}（lo{g}_{3}{{a}_{n}}^{2}+1）}$，求证对一切的正整数n都有：b1+b2+…+bn＜$\frac{2}{3}$．
16．设x，y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$，则（x+1）2+y2的最小值为（　　）
A．1B．$\frac{9}{2}$C．5D．9
13．数列{an}为等比数列，且a1+1，a3+4．a5+7成等差数列，则公差d等于3．
20．在等差数列{an}中，a3+a4+a5+a6+a7=400，则a2+a8=（　　）
A．40B．80C．160D．320
10．命题P：2016≤2017，则下列关于命题P说法正确的是．（　　）
A．命题P使用了逻辑联结词“或”，是假命题
B．命题P使用了逻辑联结词“且”，是假命题
C．命题P使用了逻辑联结词“非”，是假命题
D．命题P使用了逻辑联结词“或”，是真命题
17．如图，OABC是四面体，G是△ABC的重心，G1是OG上一点，且OG=3OG1，则（　　）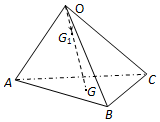
A．$\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$B．$\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$
C．$\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$D．$\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$
14．已知命题p：方程$\frac{{x}^{2}}{2m-1}$+$\frac{{y}^{2}}{m-1}$=1表示的曲线是焦点在x轴的双曲线；命题q：关于m的不等式m2-（2a+1）m+a（a+1）≤0成立．
（1）若a=$\frac{1}{2}$，且p∧q为真，求实数m的取值范围．
（2）若p是q的充分不必要条件，求实数a的取值范围．
15．方程$lnx-\frac{1}{x}=0$的实数根的所在区间为（　　）
A．（3，4）B．（2，3）C．（1，2）D．（0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网