��Ŀ����
20����֪�Ȳ�����{an}������Ϊc������Ϊd���ȱ�����{bn}������Ϊd������Ϊc������c��d��Z����a1��b1��a2��b2��a3��
��1����֤��0��c��d������b2��a3�Ƶ�c��ֵ��
��2��������{an}����3n�ǰn��ĺ�ΪA������n��ĺ�ΪB��������n��ĺ�ΪC����$\frac{{B}^{2}-AC}{��A-C��^{2}}$�ı�ֵ��
��3��������{bn}��ǰn�ǰ2n�ǰ3n��ĺͷֱ�ΪD��G��H�����ú���ĸD��G��ʽ������ʾH����H=f��D��G�����Ҳ�����ĸd��
���� ��1�����ݵȲ�ȱ����е�ͨ�ʽ������֪0��c��d�������֪����a1��b1��a2��b2��a3�г�����ʽ�飺$\left\{\begin{array}{l}{0��c��d}\\{d��cd}\\{cd��c+2d��3d}\end{array}\right.$��ͨ����ò���ʽ���Ƶ�c��ֵ��
��2�����ݵȲ����е�ͨ�ʽ��������֪A=Sn��B=S2n-Sn��C=S3n-S2n����B��A+C=2B����ϴ���ʽ�ı�������$\frac{{B}^{2}-AC}{��A-C��^{2}}$��ֵ��
��3�����ݵȱ����е�ǰn���ʽ�ֱ��ʾ��D��G��H��Ȼ���ҵ����ǵ�������ϵ��
��� �⣺��1����֪a1=c��a2=c+d��a3=c+2d��b1=d��b2=dc��
��b1��a2��֪c��0�����0��c��d��
��a1��b1��a2��b2��a3�ɵã�c��d��c+d��cd��c+2d����c��d��Z��
��˿ɵò���ʽ�飺$\left\{\begin{array}{l}{0��c��d}\\{d��cd}\\{cd��c+2d��3d}\end{array}\right.$⇒$\left\{\begin{array}{l}{0��c}\\{1��c}\\{c��3}\end{array}\right.$⇒1��c��3��
����Ϊc��Z��
���c=2��
��2������{an}��ͨ��Ϊ����an=2+��n-1��d��Sn=$\frac{d}{2}$n2+��2-$\frac{d}{2}$��n��A=Sn��B=S2n-Sn��C=S3n-S2n��
B=$\frac{d}{2}$��4n2-n2��+��2-$\frac{d}{2}$����2n-n��=$\frac{d}{2}$•3n2+��2-$\frac{d}{2}$��n��
�ɵ�A+C=$\frac{d}{2}$n2+��2-$\frac{d}{2}$��n+$\frac{d}{2}$��9n2-4n2��+��2-$\frac{d}{2}$����3n-2n��=3d•n2+��2-$\frac{d}{2}$��•2n��
�ɵ�A+C=2B��
���$\frac{{B}^{2}-AC}{��A-C��^{2}}$=$\frac{��A+C��^{2}-4AC}{4��A-C��}$=$\frac{1}{4}$��
��3������{bn}��ͨ��Ϊbn=d•2n-1��
���D=$\frac{d��{2}^{n}-1��}{2-1}$=d��2n-1����G=d��22n-1����H=d��23n-1����
����$\left\{\begin{array}{l}{G=��{2}^{n}+1��•D}\\{H=��{2}^{3n}+{2}^{n}+1��•D}\end{array}\right.$��
���H=D•��$\frac{G}{D}$-1��2+G=$\frac{{G}^{2}}{D}$+2D-G��
���� ���⿼��ȱȡ��Ȳ����е�ͨ�ʽ��Ӧ�ã����е���ͣ�������������������ѶȽϴ����Ŀ��

 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�| �·� | ������ | ú���� |
| һ�·� | 4m3 | 4Ԫ |
| ���·� | 25m3 | 14Ԫ |
| ���·� | 35m3 | 19Ԫ |
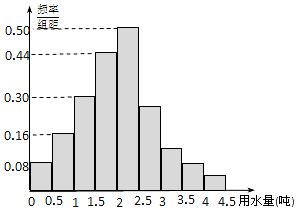 ij����100λ������˾�����ˮ������λ��t����Ƶ�ʷֲ�ֱ��ͼ��Ƶ���ֲ������£�
ij����100λ������˾�����ˮ������λ��t����Ƶ�ʷֲ�ֱ��ͼ��Ƶ���ֲ������£�| ���� | Ƶ�� |
| [0��0.5�� | 4 |
| [0.5��1�� | 8 |
| [1��1.5�� | 15 |
| [1.5��2�� | 22 |
| [2��2.5�� | 25 |
| [2.5��3�� | 14 |
| [3��3.5�� | 6 |
| [3.5��4�� | 4 |
| [4��4.5�� | 2 |
| �ϼ� | 100 |
��2�����������ƶ����˾�����ˮ��Ϊ3t�ı������������ӱ��շѣ�������������˵��85%���ϵľ������������������Ͷ���Ϊʲô��
| A�� | ����Pʹ����������ʡ����Ǽ����� | |
| B�� | ����Pʹ����������ʡ��ҡ����Ǽ����� | |
| C�� | ����Pʹ����������ʡ��ǡ����Ǽ����� | |
| D�� | ����Pʹ����������ʡ����������� |