题目内容
函数f(x)=3sin(20°+x)+5sin(x+80°)的值域为 .
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:利用两角和的正弦可求得sin(x+80°)=sin[(x+20°)+60°]=
sin(20°+x)+
cos(20°+x),再利用辅助角公式可得f(x)=7sin(20°+x+φ),于是可得其值域.
| 1 |
| 2 |
| ||
| 2 |
解答:
解:∵sin(x+80°)=sin[(x+20°)+60°]
=
sin(20°+x)+
cos(20°+x),
∴f(x)=3sin(20°+x)+5sin(x+80°)
=3sin(20°+x)+[
sin(20°+x)+
cos(20°+x)]
=
sin(20°+x)+
cos(20°+x)
=
sin(20°+x+φ)
=7sin(20°+x+φ),
∴f(x)∈[-7,7],
故答案为:[-7,7].
=
| 1 |
| 2 |
| ||
| 2 |
∴f(x)=3sin(20°+x)+5sin(x+80°)
=3sin(20°+x)+[
| 5 |
| 2 |
5
| ||
| 2 |
=
| 11 |
| 2 |
5
| ||
| 2 |
=
(
|
=7sin(20°+x+φ),
∴f(x)∈[-7,7],
故答案为:[-7,7].
点评:本题考查两角和的正弦,着重考查三角恒等变换及其应用,求得f(x)=7sin(20°+x+φ)是关键,考查转化思想与运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知直线l1:4x-3y+11=0和直线l2:x+1=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
扇形的周长是16,圆心角是2rad,则扇形的面积是( )
| A、16 | B、32 |
| C、16π | D、32π |
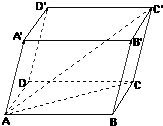 如图在平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长是
如图在平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长是