题目内容

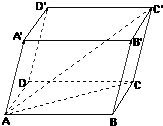如图在平行六面体ABCD-A′B′C′D′中，AB=4，AD=3，AA′=5，∠BAD=90°，∠BAA′=∠DAA′=60°，则AC′的长是
 
．
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：
.
AC′ 
2=（
AB
+
BC
+
CC′
）2，由此利用向量能求出AC′的长．
解答： 解：∵在平行六面体ABCD-A′B′C′D′中，
AB=4，AD=3，AA′=5，∠BAD=90°，
∠BAA′=∠DAA′=60°，
.
AC′ 
2=（
AB
+
BC
+
CC′
）2
=16+9+25+2×3×5×cos60°+2×4×5×cos60°
=85，
∴AC′的长是
85
．
故答案为：
85
．
点评：本题考查线段落长的求法，是基础题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
相关题目
下列四个结论：
①如果一条直线和另一条直线平行，那么它就和经过另一条直线的任何平面平行；
②如果一条直线和一个平面平行，那么它就和这个平面内的任何直线平行；
③平行于同一平面的两条直线平行；
④垂直于同一个平面的两条直线平行．
其中正确结论的序号是
 
．
极点到直线ρ（cosθ-sinθ）=2的距离为
 
．
一个盒子中装有形状大小相同的5张卡片，上面分别标有数字1，2，3，4，5，甲乙两人分别从盒子中随机不放回的各抽取一张．以盒子中剩下的三张卡片上的数字作为边长来构造三角形，则能构成三角形的概率是
 
．
如图所示，以等腰直角三角形ABC斜边BC上的高AD为折痕．使△ABD和△ACD折成互相垂直的两个平面，则∠BAC=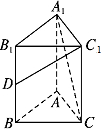
 
．
如图，直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，∠B1A1C1=90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为
 
．
函数f（x）=3sin（20°+x）+5sin（x+80°）的值域为
 
．
以（-4，0），（4，0）为焦点，y=±
3
x为渐近线的双曲线的方程为（　　）
A、
x2
4
-
y2
12
=1
B、
x2
12
-
y2
4
=1
C、
x2
24
-
y2
8
=1
D、
x2
8
-
y2
24
=1
点（1，2）在圆
x=-1+8cosθ
y=8sinθ
的（　　）
A、内部B、外部
C、圆上D、与θ的值有关

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网