题目内容
给出下列命题:
①在空间,若两条直线都与第三条直线平行,则这两条直线平行;
②在空间,若两条直线都与第三条直线垂直,则这两条直线平行;
③在空间,若两条直线都与一个平面平行,则这两条直线平行;
④在空间,若两条直线都与一个平面垂直,则这两条直线平行;
其中,正确命题的序号是 .(写出所有正确命题的序号)
①在空间,若两条直线都与第三条直线平行,则这两条直线平行;
②在空间,若两条直线都与第三条直线垂直,则这两条直线平行;
③在空间,若两条直线都与一个平面平行,则这两条直线平行;
④在空间,若两条直线都与一个平面垂直,则这两条直线平行;
其中,正确命题的序号是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①利用平行公理即可判断出;
②在空间,若两条直线都与第三条直线垂直,则这两条直线平行、相交或为异面直线;
③在空间,若两条直线都与一个平面平行,则这两条直线平行、相交或为异面直线;
④利用线面垂直的性质定理即可判断出.
②在空间,若两条直线都与第三条直线垂直,则这两条直线平行、相交或为异面直线;
③在空间,若两条直线都与一个平面平行,则这两条直线平行、相交或为异面直线;
④利用线面垂直的性质定理即可判断出.
解答:
解:①在空间,若两条直线都与第三条直线平行,则这两条直线平行,利用平行公理可知正确;
②在空间,若两条直线都与第三条直线垂直,则这两条直线平行、相交或为异面直线,因此不正确;
③在空间,若两条直线都与一个平面平行,则这两条直线平行、相交或为异面直线,因此不正确;
④在空间,若两条直线都与一个平面垂直,则这两条直线平行,利用线面垂直的性质定理可知正确.
综上可得:只有①④正确.
故答案为:①④.
②在空间,若两条直线都与第三条直线垂直,则这两条直线平行、相交或为异面直线,因此不正确;
③在空间,若两条直线都与一个平面平行,则这两条直线平行、相交或为异面直线,因此不正确;
④在空间,若两条直线都与一个平面垂直,则这两条直线平行,利用线面垂直的性质定理可知正确.
综上可得:只有①④正确.
故答案为:①④.
点评:本题考查了空间中的线线位置关系及其判定方法、平行公理、线面垂直的性质定理,考查了推理能力和空间想象能力,属于中档题.

练习册系列答案
相关题目
以(-4,0),(4,0)为焦点,y=±
x为渐近线的双曲线的方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从1,2,3,4,5,6这六个数中,不放回地任意取两个数,每次取一个数,则所取的两个数都是偶数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设A(1,3),B(-2,-3),C(x,7),若
∥
,则x的取值是( )
| AB |
| BC |
| A、18 | B、15 | C、3 | D、0 |
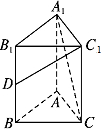 如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为