题目内容
| 1-tanA |
| 1+tanA |
| 5 |
| π |
| 4 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:直接把原等式变形求得tan(
+A)的值.
| π |
| 4 |
解答:
解:∵
=
,
∴
=
,
即
=
.
∴tan(
+A)=
.
故答案为:
.
| 1-tanA |
| 1+tanA |
| 5 |
∴
| 1+tanA |
| 1-tanA |
| ||
| 5 |
即
tan
| ||
1-tan
|
| ||
| 5 |
∴tan(
| π |
| 4 |
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:本题考查两角和的正切公式,考查了学生的灵活变形能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(5,0),
=(-2,1),
⊥
,且
=t
+
(t∈R),t=( )
| a |
| b |
| b |
| c |
| a |
| b |
| c |
| A、-2 | B、-1 | C、0 | D、2 |
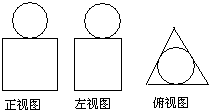
 关于下列命题:
关于下列命题: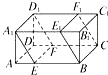 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为