题目内容
在区间[0,3]上任取实数a,在区间[0,2]上任取实数b,则使方程x2+2ax+b2=0有实数根的概率是 .
考点:古典概型及其概率计算公式,函数的零点与方程根的关系
专题:概率与统计
分析:本题是一个等可能事件的概率,试验发生包含的事件是在区间[0,3]和[0,2]上任取两个数a和b,写出事件对应的集合,做出面积,满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,根据二次方程的判别式写出a,b要满足的条件,写出对应的集合,做出面积,得到概率.
解答:
解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[0,3]和[0,2]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤3,0≤b≤2},
对应的面积是sΩ=6.
满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,
即4a2-4b2≥0,
∴a≥b,
事件对应的集合是A={(a,b)|0≤a≤3,0≤b≤2,a≥b}
对应的图形的面积是sA=4
∴根据等可能事件的概率得到P=
=
,
故答案为:
∵试验发生包含的事件是在区间[0,3]和[0,2]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤3,0≤b≤2},
对应的面积是sΩ=6.
满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,
即4a2-4b2≥0,
∴a≥b,
事件对应的集合是A={(a,b)|0≤a≤3,0≤b≤2,a≥b}
对应的图形的面积是sA=4
∴根据等可能事件的概率得到P=
| 4 |
| 6 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查几何概型,古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
△ABC中AB=2,AC=1,D为BC的中点,则
•
=( )
| AD |
| BC |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
f(x)=log2(
-x),若f(m)=n,则f(-m)=( )
| x2+1 |
| A、m+n | B、m-n |
| C、-m | D、-n |
如图为某几何体的三视图,则其体积为( )


| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
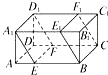 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为