题目内容
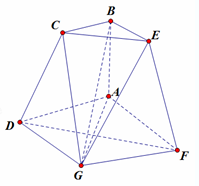 如图,ABCD与ABEF是全等的直角梯形,AB⊥AD,底面四边形ADGF为菱形,二面角D-AB-F=1200,AD=2BC=4,AB=2,
如图,ABCD与ABEF是全等的直角梯形,AB⊥AD,底面四边形ADGF为菱形,二面角D-AB-F=1200,AD=2BC=4,AB=2,(1)求证:FD⊥BG
(2)求证:CE∥DF
(3)求点A到面CEG的距离.
考点:点、线、面间的距离计算,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)由已知得AB⊥平面ADGF,AB⊥FD,又FD⊥AG,由此能证明FD⊥BG.
(2)取AD、AF的中点M,N,连结CM、MN、NE,由已知得MCEN是平行四边形,由此能证明CE∥DF.
(3)取CE中点K,连结BK,GK,过点A作AH⊥GK,则HA是点A到面CEG的距离,由此能求出点A到面CEG的距离.
(2)取AD、AF的中点M,N,连结CM、MN、NE,由已知得MCEN是平行四边形,由此能证明CE∥DF.
(3)取CE中点K,连结BK,GK,过点A作AH⊥GK,则HA是点A到面CEG的距离,由此能求出点A到面CEG的距离.
解答:
(1)证明:∵AB⊥AD,AB⊥AF,AD∩AF=A,
∴AB⊥平面ADGF,AB⊥FD,又FD⊥AG,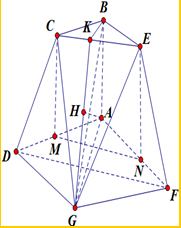
∴FD⊥面ABG,∴FD⊥BG.
(2)证明:取AD、AF的中点M,N,连结CM、MN、NE,
CM∥AB∥NE,∴MCEN是平行四边形,
∴CE∥MN,而MN∥DF,
∴CE∥DF.
(3)解:如图,取CE中点K,连结BK,GK,
过点A作AH⊥GK,
由(1)可证CE∥DF,DF⊥平面ABKG,
∴CE⊥面ABKG,∴CE⊥HA,HA⊥面CEG,
∴HA是点A到面CEG的距离,
∵二面角D-AB-F=120°,AD=2BC=4,AB=2,
∴BK=1,AG=2,GK=
,
∵
GK•AH=
GA•AB,
∴HA=
=
=
.
∴AB⊥平面ADGF,AB⊥FD,又FD⊥AG,

∴FD⊥面ABG,∴FD⊥BG.
(2)证明:取AD、AF的中点M,N,连结CM、MN、NE,
CM∥AB∥NE,∴MCEN是平行四边形,
∴CE∥MN,而MN∥DF,
∴CE∥DF.
(3)解:如图,取CE中点K,连结BK,GK,
过点A作AH⊥GK,
由(1)可证CE∥DF,DF⊥平面ABKG,
∴CE⊥面ABKG,∴CE⊥HA,HA⊥面CEG,
∴HA是点A到面CEG的距离,
∵二面角D-AB-F=120°,AD=2BC=4,AB=2,
∴BK=1,AG=2,GK=
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴HA=
| GA•AB |
| GK |
| 2×2 | ||
|
4
| ||
| 5 |
点评:本题考查异面直线垂直的证明,考查直线与直线平行的证明,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知F1、F2分别是双曲线x2-my2=1(m>0)的左、右焦点,P为双曲线左支上任意一点,若
的最小值为8,则双曲线的离心率的取值范围为( )
|
| ||
|
|
| A、(1,3] |
| B、(0,3] |
| C、(1,2] |
| D、(1,+∞) |