题目内容

已知△ABC的顶点B、C在椭圆
x2
3
+y2=1上，顶点A是椭圆的一个焦点，且BC边经过椭圆的另外一个焦点，则△ABC的周长是（　　）
A、2
3
B、4
3
C、6
D、3
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设另一个焦点为F，根据椭圆的定义可知|AB|+|BF|=2a，|AC|+|FC|=2a最后把这四段线段相加求得△ABC的周长．
解答： 解：椭圆
x2
3
+y2=1的a=
3
．
设另一个焦点为F，则根据椭圆的定义可知
|AB|+|BF|=2a=2
3
，|AC|+|FC|=2a=2
3
．
∴三角形的周长为：|AB|+|BF|+|AC|+|FC|=4
3
．
故选：B．
点评：本题主要考查数形结合的思想和椭圆的基本性质，解题的关键是利用椭圆的第一定义．
练习册系列答案
相关题目
已知随机变量ξ的分布列如表所示，则D（ξ）=
 
．
ξ012
p
1
2
a
1
4
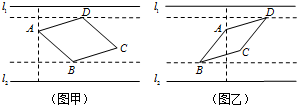如图，某兴趣小组测得菱形养殖区ABCD的固定投食点A到两条平行河岸线l1、l2的距离分别为4米、8米，河岸线l1与该养殖区的最近点D的距离为1米，l2与该养殖区的最近点B的距离为2米．
（1）如图甲，养殖区在投食点A的右侧，若该小组测得∠BAD=60°，请据此算出养殖区的面积S，并求出直线AD与直线l1所成角的正切值；
（2）如图乙，养殖区在投食点A的两侧，试求养殖区面积S的最小值，并求出取得最小值时∠BAD的余弦值．
双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）与直线y=a相交所得的线段长为2b，则该双曲线的离心率的平方为
 
．
已知函数f（x）=
1
(x+1)ln(x+1)
．
（I）求函数f（x）的单调区间；
（Ⅱ）是否存在实数m，使不等式
1
x+1
ln2＞mln（x+1）在-1＜x＜0时恒成立？若存在，求出实数m的取值范围；若不存在，请说明理由．
（Ⅲ）已知正整数列{cn}中，(Cn)(n+1)2=e
1
f(n)
(n∈N*)，求数列{cn}中的最大项．
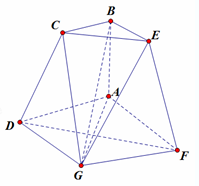如图，ABCD与ABEF是全等的直角梯形，AB⊥AD，底面四边形ADGF为菱形，二面角D-AB-F=1200，AD=2BC=4，AB=2，
（1）求证：FD⊥BG
（2）求证：CE∥DF
（3）求点A到面CEG的距离．
已知点P是椭圆
x2
16
+
y2
7
=1上的动点，M为过P且垂直于x轴的直线上的点，
|OP|
|OM|
=λ．求点M的轨迹方程，并说明轨迹是什么曲线．
等差数列{an}的前n项和为Sn，若a2+a7+a12=60，则S13的值是（　　）
A、130B、260
C、20D、150
已知{1，2，3}是集合M的真子集，M是{1，2，3，4，5，6}的真子集，求符合M的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网