��Ŀ����
��֪����{an}�Ǹ����Ϊ�����ĵȲ����У�
��1����a1=2����a2��a3��a4+1�ɵȱ����У�������{an}��ͨ�ʽan��
��2���ڣ�1���������£�����{an}��ǰn��ΪSn����bn=
+
+��+
�����������n����������ʽbn��k���������ʵ��k����Сֵ��
��3��������{an}����������Ա�ʾΪij������c��c��1���IJ�ͬ���ݣ���֤������{an}�д����������ɵȱ����У�
��1����a1=2����a2��a3��a4+1�ɵȱ����У�������{an}��ͨ�ʽan��
��2���ڣ�1���������£�����{an}��ǰn��ΪSn����bn=
| 1 |
| Sn+1 |
| 1 |
| Sn+2 |
| 1 |
| S2n |
��3��������{an}����������Ա�ʾΪij������c��c��1���IJ�ͬ���ݣ���֤������{an}�д����������ɵȱ����У�
���㣺�����벻��ʽ���ۺ�
ר�⣺�Ȳ�������ȱ�����
��������1������֪��a32=a2��a4+1����d��0���ɴ����������{an}��ͨ�ʽan=2n��
��2����Sn=n��n+1������bn=
+
+��+
=
��Ҫʹ�������������n������ʽbn��k���������ʹk��[bn]max=
���ɴ������ʵ��k����Сֵ��10�֣�
��3����cr=ai��cs=aj������ai��aj �����е��a�Ǵ���1��������r��s��i��j����t=s-r����cs-cr=cS-cr=cr��ct-1�����ɴ���֤������{an}�д����������ɵȱ����У�
��2����Sn=n��n+1������bn=
| 1 |
| Sn+1 |
| 1 |
| Sn+2 |
| 1 |
| S2n |
| 1 | ||
2n+
|
| 1 |
| 6 |
��3����cr=ai��cs=aj������ai��aj �����е��a�Ǵ���1��������r��s��i��j����t=s-r����cs-cr=cS-cr=cr��ct-1�����ɴ���֤������{an}�д����������ɵȱ����У�
���
��1���⣺��Ϊa1=2����a2��a3��a4+1�ɵȱ����У�
����a1=2��a32=a2��a4+1��������Ϊ{an}������Ȳ����У���d��0
���ԣ�2+2d��2=��2+d����3+3d������d=2��d=1����ȥ����
��������{an}��ͨ�ʽan=2n������4�֣�
��2���⣺��ΪSn=n��n+1����
bn=
+
+��+
=
+
+��+
=
-
+
-
+��+
-
=
-
=
=
��
��f(x)=2x+
��x��1������f�䣨x��=2x-
����xx��1ʱ��f�䣨x����0�������
����f��x����[1��+�ޣ�������������
�ʵ�x=1ʱ��[f��x��]min=f��1��=3������n=1ʱ��[bn]max=
��
Ҫʹ�������������n������ʽbn��k�������
����ʹk��[bn]max=
������ʵ��k����СֵΪ
������10�֣�
��3��֤������Ϊ������е�����������������Ҳ���ȣ�����d��0��
��cr=ai��cs=aj������ai��aj �����е��a�Ǵ���1��������r��s��i��j��
��t=s-r����cs-cr=cS-cr=cr��ct-1����
��cs-cr=aj-ai��d������������c��r+kt����cc+kl��
����cr+kl-cr=cr��ckt-1��=cr��ct-1����c��k-l��t+k+1�����ұ���d����������
����cr+kt������ʽ������{an}��ijһ�
����еȱ�����{bn}������b1=cr��q=ct=c5-r�� ����16�֣�
����a1=2��a32=a2��a4+1��������Ϊ{an}������Ȳ����У���d��0
���ԣ�2+2d��2=��2+d����3+3d������d=2��d=1����ȥ����
��������{an}��ͨ�ʽan=2n������4�֣�
��2���⣺��ΪSn=n��n+1����
bn=
| 1 |
| Sn+1 |
| 1 |
| Sn+2 |
| 1 |
| S2n |
| 1 |
| (n+1)(n+2) |
| 1 |
| (n+2)(n+3) |
| 1 |
| 2n(2n+1) |
=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
=
| 1 |
| n+1 |
| 1 |
| 2n |
=
| n |
| 2n2+3n+1 |
=
| 1 | ||
2n+
|
��f(x)=2x+
| 1 |
| x |
| 1 |
| x2 |
����f��x����[1��+�ޣ�������������
�ʵ�x=1ʱ��[f��x��]min=f��1��=3������n=1ʱ��[bn]max=
| 1 |
| 6 |
Ҫʹ�������������n������ʽbn��k�������
����ʹk��[bn]max=
| 1 |
| 6 |
| 1 |
| 6 |
��3��֤������Ϊ������е�����������������Ҳ���ȣ�����d��0��
��cr=ai��cs=aj������ai��aj �����е��a�Ǵ���1��������r��s��i��j��
��t=s-r����cs-cr=cS-cr=cr��ct-1����
��cs-cr=aj-ai��d������������c��r+kt����cc+kl��
����cr+kl-cr=cr��ckt-1��=cr��ct-1����c��k-l��t+k+1�����ұ���d����������
����cr+kt������ʽ������{an}��ijһ�
����еȱ�����{bn}������b1=cr��q=ct=c5-r�� ����16�֣�
���������⿼�����е�ͨ�ʽ��������ʵ������Сֵ��������ȱ����е�֤��������Ҫע�ⲻ��ʽ���ʺ�����֪ʶ�ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
��f��x���Ƕ����ڣ�-�ޣ�+�ޣ��Ͽɵ�����������xf'��x��+f��x����0�����������a��b����a��b�����в���ʽ��������ǣ�������
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
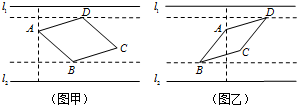 ��ͼ��ij��ȤС����������ֳ��ABCD�Ĺ̶�Ͷʳ��A������ƽ�кӰ���l1��l2�ľ���ֱ�Ϊ4�ס�8�ף��Ӱ���l1�����ֳ���������D�ľ���Ϊ1�ף�l2�����ֳ���������B�ľ���Ϊ2�ף�
��ͼ��ij��ȤС����������ֳ��ABCD�Ĺ̶�Ͷʳ��A������ƽ�кӰ���l1��l2�ľ���ֱ�Ϊ4�ס�8�ף��Ӱ���l1�����ֳ���������D�ľ���Ϊ1�ף�l2�����ֳ���������B�ľ���Ϊ2�ף� ����P-ABCD�У�����ABCD�DZ߳�Ϊ2�������Σ�PB��BC��PD��CD��E�Dz���PD���е㣮
����P-ABCD�У�����ABCD�DZ߳�Ϊ2�������Σ�PB��BC��PD��CD��E�Dz���PD���е㣮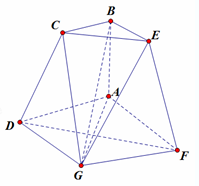 ��ͼ��ABCD��ABEF��ȫ�ȵ�ֱ�����Σ�AB��AD�������ı���ADGFΪ���Σ������D-AB-F=1200��AD=2BC=4��AB=2��
��ͼ��ABCD��ABEF��ȫ�ȵ�ֱ�����Σ�AB��AD�������ı���ADGFΪ���Σ������D-AB-F=1200��AD=2BC=4��AB=2�� ��ƽ��ֱ������ϵxOy������Ǧ���ʼ����x��ķǸ������غϣ��ձ��뵥λԲ���ڵ�P��x1��y1����������OP������ԭ��O����ʱ�뷽����ת
��ƽ��ֱ������ϵxOy������Ǧ���ʼ����x��ķǸ������غϣ��ձ��뵥λԲ���ڵ�P��x1��y1����������OP������ԭ��O����ʱ�뷽����ת