题目内容
下列叙述:
①函数y=
在(-∞,0)∪(0,+∞)上是减函数;
②已知集合P={a,b},Q={-1,0.1},则映射f:P→Q中满足f(b)=0的映射共有3个;
③对于函数f(x)=-x2+1,当x1≠x2时,都有
<f(
);
④若函数f(x)=
在R上是增函数,则m的取值范围是1<m<2;
其中正确的所有番号是: .
①函数y=
| 1 |
| x |
②已知集合P={a,b},Q={-1,0.1},则映射f:P→Q中满足f(b)=0的映射共有3个;
③对于函数f(x)=-x2+1,当x1≠x2时,都有
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
④若函数f(x)=
|
其中正确的所有番号是:
考点:命题的真假判断与应用
专题:简易逻辑
分析:举例说明①错误;由映射概念说明②正确;f(x)=-x2+1,x1≠x2,利用作差法能够比较
和f(
)的大小说明③正确;由增函数的概念列不等式组求解m的范围说明④错误.
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
解答:
解:①函数y=
在(-∞,0)∪(0,+∞)上是减函数错误,如1>-1,f(1)>f(-1);
②已知集合P={a,b},Q={-1,0.1},则映射f:P→Q中满足f(b)=0的映射共有3个正确,原因是f(b)=0一定,而f(a)可以对应-1、0、1有三种对应法;
③对于函数f(x)=-x2+1,当x1≠x2时,都有
<f(
)正确.
∵f(x)=-x2+1,x1≠x2,
∴
-f(
)=
-[-(
)2+1]=
-
<0,
∴
<f(
),故③正确;
④若函数f(x)=
在R上是增函数,则
,解得
≤m<2,命题④错误.
故答案为:②③.
| 1 |
| x |
②已知集合P={a,b},Q={-1,0.1},则映射f:P→Q中满足f(b)=0的映射共有3个正确,原因是f(b)=0一定,而f(a)可以对应-1、0、1有三种对应法;
③对于函数f(x)=-x2+1,当x1≠x2时,都有
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
∵f(x)=-x2+1,x1≠x2,
∴
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| -x12+1-x22+1 |
| 2 |
| x1+x2 |
| 2 |
| x12+2x1x2+x22 |
| 4 |
| x12+x22 |
| 2 |
∴
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
④若函数f(x)=
|
|
| 5 |
| 4 |
故答案为:②③.
点评:本题考查了命题的真假判断与应用,考查了函数的性质及其应用,是中档题.

练习册系列答案
相关题目
定义在R上的函数f(x)满足f(x+2)=
f(x),当x∈[0,2]时,f(x)=
函数g(x)=x3+3x2+m,若?s∈[-4,2),?t∈[-4,-2),不等式f(s)-g(t)≥0,则实数m的取值范围是( )
| 1 |
| 2 |
|
| A、(-∞,-12] | ||
| B、(-∞,-4] | ||
| C、(-∞,8] | ||
D、(-∞,
|
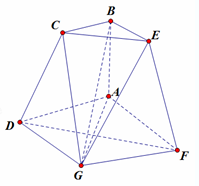 如图,ABCD与ABEF是全等的直角梯形,AB⊥AD,底面四边形ADGF为菱形,二面角D-AB-F=1200,AD=2BC=4,AB=2,
如图,ABCD与ABEF是全等的直角梯形,AB⊥AD,底面四边形ADGF为菱形,二面角D-AB-F=1200,AD=2BC=4,AB=2, 在平面直角坐标系xOy中设锐角α的始边与x轴的非负半轴重合,终边与单位圆交于点P(x1,y1),将射线OP绕坐标原点O按逆时针方向旋转
在平面直角坐标系xOy中设锐角α的始边与x轴的非负半轴重合,终边与单位圆交于点P(x1,y1),将射线OP绕坐标原点O按逆时针方向旋转
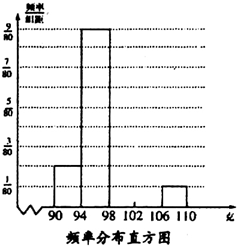 为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图:
为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图: