题目内容
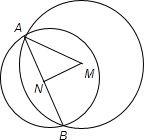
已知圆M:x2+y2-2mx+4y+m2-1=0与圆N:x2+y2+2x+2y-2=0相交于A,B两点,且这两点平分圆N的圆周,求圆M的圆心坐标.
考点:圆与圆的位置关系及其判定
专题:计算题,直线与圆
分析:由题意在Rt△AMN中,|AM|2=|AN|2+|MN|2,即可求圆M的圆心坐标.
解答:
 解:由题意,圆M的圆心坐标为(m,-2),半径为
解:由题意,圆M的圆心坐标为(m,-2),半径为
圆N的圆心N(-1,-1),半径为2,N为弦AB的中点,
在Rt△AMN中,|AM|2=|AN|2+|MN|2,
∴5=4+(m+1)2+1,
∴m=-1,
∴圆M的圆心坐标为(-1,-2).
 解:由题意,圆M的圆心坐标为(m,-2),半径为
解:由题意,圆M的圆心坐标为(m,-2),半径为| 5 |
圆N的圆心N(-1,-1),半径为2,N为弦AB的中点,
在Rt△AMN中,|AM|2=|AN|2+|MN|2,
∴5=4+(m+1)2+1,
∴m=-1,
∴圆M的圆心坐标为(-1,-2).
点评:本小题主要考查圆与圆的位置关系,考查运用数学知识解决问题的能力,比较基础.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
等差数列{an}的前n项和为Sn,若a2+a7+a12=60,则S13的值是( )
| A、130 | B、260 |
| C、20 | D、150 |
定义在R上的函数f(x)满足f(x+2)=
f(x),当x∈[0,2]时,f(x)=
函数g(x)=x3+3x2+m,若?s∈[-4,2),?t∈[-4,-2),不等式f(s)-g(t)≥0,则实数m的取值范围是( )
| 1 |
| 2 |
|
| A、(-∞,-12] | ||
| B、(-∞,-4] | ||
| C、(-∞,8] | ||
D、(-∞,
|
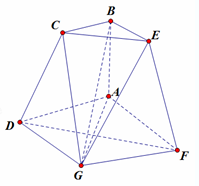 如图,ABCD与ABEF是全等的直角梯形,AB⊥AD,底面四边形ADGF为菱形,二面角D-AB-F=1200,AD=2BC=4,AB=2,
如图,ABCD与ABEF是全等的直角梯形,AB⊥AD,底面四边形ADGF为菱形,二面角D-AB-F=1200,AD=2BC=4,AB=2, 在平面直角坐标系xOy中设锐角α的始边与x轴的非负半轴重合,终边与单位圆交于点P(x1,y1),将射线OP绕坐标原点O按逆时针方向旋转
在平面直角坐标系xOy中设锐角α的始边与x轴的非负半轴重合,终边与单位圆交于点P(x1,y1),将射线OP绕坐标原点O按逆时针方向旋转