题目内容
已知F1、F2分别是双曲线x2-my2=1（m＞0）的左、右焦点，P为双曲线左支上任意一点，若
的最小值为8，则双曲线的离心率的取值范围为（ ）
|
| ||
|
|
| A、（1，3] |
| B、（0，3] |
| C、（1，2] |
| D、（1，+∞） |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先利用双曲线的定义求出关系式，进一步利用均值不等式建立关系式，
=
≥8，最后求出结果．
|
| ||
|
|
| (2+n)2 |
| n |
解答：
解：设|PF2|=n，（n≥c-1）
则：根据双曲线的定义：|PF1|=2+n，
则：
=
≥8，
当且仅当n=2时成立．
所以：c-1≤2，即1＜c≤3
即解得：1＜e≤3
双曲线的离心率的取值范围为：（1，3]，
故选：A
则：根据双曲线的定义：|PF1|=2+n，
则：
|
| ||
|
|
| (2+n)2 |
| n |
当且仅当n=2时成立．
所以：c-1≤2，即1＜c≤3
即解得：1＜e≤3
双曲线的离心率的取值范围为：（1，3]，
故选：A
点评：本题考查的知识要点：双曲线的定义的应用．双曲线的离心率，均值不等式的应用，属于中等题型．
练习册系列答案
阅读快车系列答案
相关题目
已知a的第四象限的角，且sin（
+α）=
，则tanα=（ ）
| π |
| 2 |
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的渐近线方程是y=±
x．
（1）求该双曲线的离心率；
（2）若点P（2，1）在双曲线E上，求直线y=kx+1与该双曲线有且仅有一个公共点时相应的k值．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
（1）求该双曲线的离心率；
（2）若点P（2，1）在双曲线E上，求直线y=kx+1与该双曲线有且仅有一个公共点时相应的k值．
设f（x）是定义在（-∞，+∞）上可导函数且满足xf'（x）+f（x）＞0对任意的正数a，b，若a＞b则下列不等式恒成立的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
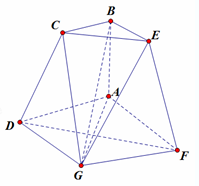如图，ABCD与ABEF是全等的直角梯形，AB⊥AD，底面四边形ADGF为菱形，二面角D-AB-F=1200，AD=2BC=4，AB=2，