题目内容
4.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线的离心率乘积的最小值为( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
分析 先设椭圆的长半轴长为a1,双曲线的半实轴长a2,焦距2c.因为涉及椭圆及双曲线离心率的问题,所以需要找a1,a2,c之间的关系,而根据椭圆及双曲线的定义可以用a1,a2表示出|PF1|,|PF2|,在△F1PF2中根据余弦定理可得到:$\frac{1}{{{e}_{1}}^{2}}$+$\frac{3}{{{e}_{2}}^{2}}$=4,利用基本不等式可得结论.
解答 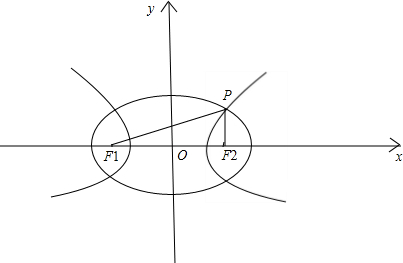 解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:
解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:
|PF1|+|PF2|=2a1,
|PF1|-|PF2|=2a2,
∴|PF1|=a1+a2,|PF2|=a1-a2,
设|F1F2|=2c,∠F1PF2=$\frac{π}{3}$,则:
在△PF1F2中由余弦定理得,
4c2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos$\frac{π}{3}$
∴化简可变成:$\frac{1}{{{e}_{1}}^{2}}$+$\frac{3}{{{e}_{2}}^{2}}$=4,
∴$\frac{1}{{{e}_{1}}^{2}}$+$\frac{3}{{{e}_{2}}^{2}}$=4≥$\frac{2\sqrt{3}}{{e}_{1}{e}_{2}}$
∴e1e2≥$\frac{\sqrt{3}}{2}$,
故选B.
点评 本题考查圆锥曲线的共同特征,考查通过椭圆与双曲线的定义求焦点三角形三边长,解决本题的关键是根据所得出的条件灵活变形,求出焦点三角形的边长来.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
12.向量$\overrightarrow{a}$=(2,4,x),$\overrightarrow{b}$=(2,y,2),若|$\overrightarrow{a}$|=6,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x+y的值为( )
| A. | -3 | B. | 1 | C. | -3或1 | D. | 3或1 |
19.已知$\frac{sinx+1}{cosx}=\frac{1}{2}$,则$\frac{sinx-1}{cosx}$的值是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
11.已知m,n是两条不同直线α,β是两个不同平面,则下列命题正确的是( )
| A. | 若α,β垂直于同一平面,则α与β平行 | |
| B. | 若m,n平行于同一平面,则m与n平行 | |
| C. | 若m,n不平行,则m与n不可能垂直于同一平面 | |
| D. | 若α,β不平行,则在α内不存在与β平行的直线 |