题目内容
15.已知抛物线关于x轴对称,顶点在坐标原点,点P(1,2),A,B均在抛物线上,(1)求该抛物线的标准方程;
(2)若线段AB的中点为(1,-1),求直线AB的方程.
分析 (1)设抛物线的方程为y2=2px.由点P(1,2)在抛物线上,求出p=2.由此能求出抛物线的方程和准线方程.
(2)设AB的方程与抛物线方程联立得k2x2+(2kb-4)x+b2=0,由此利用线段AB的中点为(1,-1),求直线AB的方程.
解答 解:(1)由已知条件,
可设抛物线的方程为y2=2px.
∵点P(1,2)在抛物线上,
∴22=2p×1,解得p=2.
故所求抛物线的方程是y2=4x;
(2)设直线AB的方程为y=kx+b,则设A(x1,y1),B(x2,y2)
联立方程组$\left\{{\begin{array}{l}{y=kx+b}\\{{y^2}=4x}\end{array}}\right.$,消去y可得k2x2+(2kb-4)x+b2=0
得${x_1}+{x_2}=\frac{4-2kb}{k^2}$,
又$\left\{{\begin{array}{l}{{x_1}+{x_2}=2}\\{k+b=-1}\end{array}}\right.$,故解得k=-2,b=1,
所以直线AB的方程为y=-2x+1.
点评 本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点,易错点是知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
5.已知i是虚数单位,复数z=m-1+(m+1)i,(其中m∈R)是纯虚数,则m=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
6.已知x,y满足$\left\{\begin{array}{l}y≤x\\ x+y+2≥0\\ x≤1\end{array}\right.$,且z=y-2x的最大值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
3.如图,A,B是以点C为圆心,R为半径的圆上的任意两个点,且|AB|=4,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )


| A. | 16 | B. | 8 | C. | 4 | D. | 与R有关的值 |
10.下列图形中,不可能是函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
20.已知双曲线$\frac{x^2}{m}+{y^2}=1$的离心率是$\sqrt{2}$,则实数m的值为( )
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
4.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线的离心率乘积的最小值为( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
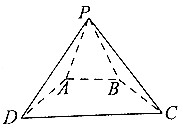 已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.
已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.