题目内容
14.已知实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ x≥\frac{1}{2}\\ y≥x\end{array}\right.$,且数列6x,z,2y为等差数列,则实数z的最大值是4.分析 画出满足条件的平面区域,求出角点的坐标,根据z=3x+y,得:y=-3x+z,显然直线过A(1,1)时,z最大,求出即可.
解答 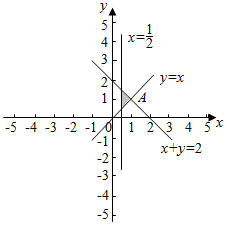 解:画出满足条件$\left\{\begin{array}{l}x+y≤2\\ x≥\frac{1}{2}\\ y≥x\end{array}\right.$的平面区域,如图示:
解:画出满足条件$\left\{\begin{array}{l}x+y≤2\\ x≥\frac{1}{2}\\ y≥x\end{array}\right.$的平面区域,如图示:
由$\left\{\begin{array}{l}{y=x}\\{x+y=2}\end{array}\right.$,解得A(1,1),
∵数列6x,z,2y为等差数列,
∴z=3x+y,得:y=-3x+z,
显然直线过A(1,1)时,z最大,z的最大值是:4,
故答案为:4.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
5.已知i是虚数单位,复数z=m-1+(m+1)i,(其中m∈R)是纯虚数,则m=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
2.已知函数f(x)=ex-e-x+4sin3x+1,x∈(-1,1),若f(1-a)+f(1-a2)>2成立,则实数a的取值范围是( )
| A. | (-2,1) | B. | (0,1) | C. | $({1,\sqrt{2}})$ | D. | (-∞,-2)∪(1,+∞) |
6.已知x,y满足$\left\{\begin{array}{l}y≤x\\ x+y+2≥0\\ x≤1\end{array}\right.$,且z=y-2x的最大值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
3.如图,A,B是以点C为圆心,R为半径的圆上的任意两个点,且|AB|=4,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )


| A. | 16 | B. | 8 | C. | 4 | D. | 与R有关的值 |
4.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线的离心率乘积的最小值为( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
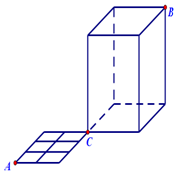 如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.
如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.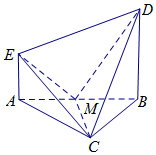 如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.
如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.