题目内容
16.已知函数f(x)=|x-a|-$\frac{1}{2}$x,(a>0).(Ⅰ)若a=3,解关于x的不等式f(x)<0;
(Ⅱ)若对于任意的实数x,不等式f(x)-f(x+a)<a2+$\frac{a}{2}$恒成立,求实数a的取值范围.
分析 (Ⅰ)将a的值带入f(x),两边平方求出不等式的解集即可;
(Ⅱ)求出f(x)=|x-a|-|x|+$\frac{a}{2}$,原问题等价于|a|<a2,求出a的范围即可.
解答 解:(Ⅰ)a=3时,f(x)=|x-3|-$\frac{1}{2}$x<0,
即|x-3|<$\frac{1}{2}$x,
两边平方得:(x-3)2<$\frac{1}{4}$x2,
解得:2<x<6,
故不等式的解集是{x|2<x<6};
(Ⅱ)f(x)-f(x+a)
=|x-a|-$\frac{1}{2}$x-|x|+$\frac{1}{2}$(x+a)
=|x-a|-|x|+$\frac{a}{2}$,
若对于任意的实数x,不等式f(x)-f(x+a)<a2+$\frac{a}{2}$恒成立,
即|x-a|-|x|+$\frac{a}{2}$<a2+$\frac{a}{2}$对x∈R恒成立,
即a2>|x-a|-|x|,而|x-a|-|x|≤|(x-a)-x|=|a|,
原问题等价于|a|<a2,又a>0,
∴a<a2,解得a>1.
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
6.已知x,y满足$\left\{\begin{array}{l}y≤x\\ x+y+2≥0\\ x≤1\end{array}\right.$,且z=y-2x的最大值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
4.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线的离心率乘积的最小值为( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
11.执行如图所示的程序框图,则输出的S的值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
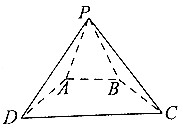 已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.
已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.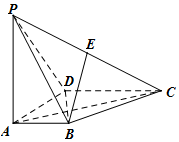 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.