题目内容
11.已知m,n是两条不同直线α,β是两个不同平面,则下列命题正确的是( )| A. | 若α,β垂直于同一平面,则α与β平行 | |
| B. | 若m,n平行于同一平面,则m与n平行 | |
| C. | 若m,n不平行,则m与n不可能垂直于同一平面 | |
| D. | 若α,β不平行,则在α内不存在与β平行的直线 |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A,若α,β垂直于同一平面,则α与β平行或相交,不正确;
对于B,若m,n平行于同一平面,则m与n平行、相交或异面,不正确;
对于C,根据垂直与同一平面的两条直线平行,可知C正确;
对于D,若α,β不平行,则在α内存在与β平行的直线,与交线平行即可,不正确,
故选:C.
点评 本题考查空间的线面位置关系,考查空间想象能力和逻辑推理能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线的离心率乘积的最小值为( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
6.已知g(x)=sin2x,将g(x)的图象向左平移$\frac{π}{8}$个单位长度,再将图象上各点的横坐标缩短到原来的$\frac{1}{4}$,得到函数f(x)的图象,则( )
| A. | $f(x)=sin(8x-\frac{π}{4})$ | B. | $f(x)=sin(8x+\frac{π}{4})$ | C. | $f(x)=sin(\frac{x}{2}-\frac{π}{4})$ | D. | $f(x)=sin(\frac{x}{2}+\frac{π}{4})$ |
16.已知p:x2-4x-5>0,q:x2-2x+1-λ2>0,若p是q的充分不必要条件,则正实数λ的取值范围是( )
| A. | (0,1] | B. | (0,2) | C. | $({0,\frac{3}{2}}]$ | D. | (0,2] |
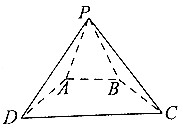 已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.
已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.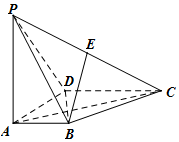 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.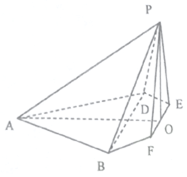 在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.
在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.