题目内容
11．某班从7名学生中选4人分别担任班长、副班长、学习委员、劳动委员四项不同的工作，若其中甲、乙两名不能担任学习委员，则不同的选法种数为（ ）| A． | 240 | B． | 500 | C． | 600 | D． | 450 |
分析 由题意知这是一个计数问题，先从除甲乙之外的5名学生中选1人担任学习委员，再从6人选人选3人安排担任班长、副班长、劳动委员，得到结果．
解答 解：先从除甲乙之外的5名学生中选1人担任学习委员，再从6人选人选3人安排担任班长、副班长、劳动委员，故有C51A63=600人
故选C．
点评 本题考查计数原理，最主要的是看清条件中对于元素的限制，注意写出是做到不重不漏．
练习册系列答案
出彩同步大试卷系列答案
相关题目
2．已知曲线C的方程为$\frac{x^2}{a^2}-{y^2}$=1（a∈R且a≠0），则“a＞1”是“曲线C是焦点在x轴上的双曲线”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
19．阅读如图的程序框图，运行相应的程序，则输出的S的值为（ ）
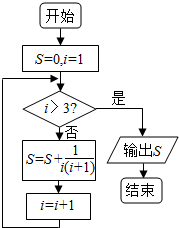
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{5}$ |
3．已知函数f（x）=e|x|-$\frac{1}{{x}^{2}}$，设a=sin2，b=cos2，c=tan2，则（ ）
| A． | f（a）＜f（b）＜f（c） | B． | f（c）＜f（b）＜f（a） | C． | f（c）＜f（a）＜f（b） | D． | f（b）＜f（a）＜f（c） |
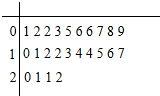为调查了解某药物使用后病人的康复时间，从1000个使用该药的病人的康复时间中抽取了24个样本，数据如下图中的茎叶图（单位：周）．专家指出康复时间在7周之内（含7周）是快效时间．