题目内容
3.已知函数f(x)=e|x|-$\frac{1}{{x}^{2}}$,设a=sin2,b=cos2,c=tan2,则( )| A. | f(a)<f(b)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(a)<f(c) |
分析 先判断出函数的单调性和奇偶性,从而判断出函数值的大小即可.
解答 解:∵函数f(x)=e|x|-$\frac{1}{{x}^{2}}$,
∴f(-x)=f(x),是偶函数,
x>0时:f(x)=ex-$\frac{1}{{x}^{2}}$,f′(x)=ex+$\frac{2}{{x}^{3}}$>0,
∴f(x)在(0,+∞)递增,
而|cos2|<|sin2|<|tan2|,
故f(b)<f(a)<f(c),
故选:D.
点评 本题考察了函数的单调性、奇偶性问题,是一道基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
11.某班从7名学生中选4人分别担任班长、副班长、学习委员、劳动委员四项不同的工作,若其中甲、乙两名不能担任学习委员,则不同的选法种数为( )
| A. | 240 | B. | 500 | C. | 600 | D. | 450 |
8.已知复数z满足$\frac{z-1}{z+1}=i$,则z等于( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
12.把函数f(x)=2sin(2x+$\frac{π}{6}$)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)的图象,关于函数g(x),下列说法正确的是( )
| A. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | |
| B. | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
13.函数y=loga2(x2-2x-3),当x<-1时为增函数,则a的取值范围是( )
| A. | a>1 | B. | -1<a<1 | C. | -1<a<1且a≠0 | D. | a>1或a<-1 |
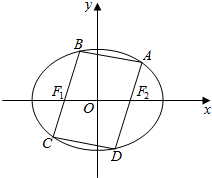 如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.
如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.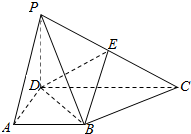 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.