题目内容
20.命题:“?x∈Q,x2-8=0”的否定是?x∈Q,x2-8≠0.分析 利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,所以命题:“?x∈Q,x2-8=0”的否定是:?x∈Q,x2-8≠0.
故答案为:?x∈Q,x2-8≠0.
点评 本题考查命题的否定全称命题与特称命题的否定关系,是基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
10.若直线(a+1)x+2y=0与直线x-ay=1互相垂直,则实数a的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
11.某班从7名学生中选4人分别担任班长、副班长、学习委员、劳动委员四项不同的工作,若其中甲、乙两名不能担任学习委员,则不同的选法种数为( )
| A. | 240 | B. | 500 | C. | 600 | D. | 450 |
8.已知复数z满足$\frac{z-1}{z+1}=i$,则z等于( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
5.要得到y=cosx-$\sqrt{3}$sinx的图象,只需将y=2sinx( )
| A. | 向左平移$\frac{5π}{6}$个单位长度 | B. | 向右平移$\frac{5π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
12.把函数f(x)=2sin(2x+$\frac{π}{6}$)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)的图象,关于函数g(x),下列说法正确的是( )
| A. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | |
| B. | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
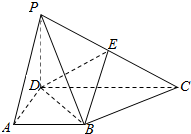 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.