题目内容
过椭圆
+
=1(a>b>0)左焦点F1作垂直于x轴的直线交椭圆于AB两点,若△ABF2为等边三角形,则该椭圆离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据△ABF2是正三角形,且直线AB与椭圆长轴垂直,得到F2F1是正三角形△ABF2的高,∠AF2F1=30°.在Rt△AF2F1中,设|AF1|=m,可得
=
,所以|AF2|=2m,用勾股定理算出|F1F2|=
m,得到椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c=
m,从而可求椭圆的离心率.
| |AF1| |
| |AF2| |
| 1 |
| 2 |
| 3 |
| 3 |
解答:
解:∵△ABF2是正三角形,
∴∠AF2B=60°,
∵直线AB与椭圆长轴垂直,
∴F2F1是正三角形△ABF2的高,∠AF2F1=
×60°=30°,
Rt△AF2F1中,设|AF1|=m,sin30°=
=
,
∴|AF2|=2m,|F1F2|=
m
因此,椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c=
m
∴椭圆的离心率为e=
=
.
故选:B.

∴∠AF2B=60°,
∵直线AB与椭圆长轴垂直,
∴F2F1是正三角形△ABF2的高,∠AF2F1=
| 1 |
| 2 |
Rt△AF2F1中,设|AF1|=m,sin30°=
| |AF1| |
| |AF2| |
| 1 |
| 2 |
∴|AF2|=2m,|F1F2|=
| 3 |
因此,椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c=
| 3 |
∴椭圆的离心率为e=
| c |
| a |
| ||
| 3 |
故选:B.
点评:本题给出椭圆过焦点垂直于长轴的弦和另一焦点构成直角三角形,求椭圆的离心率.着重考查了椭圆的基本概念和简单几何性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知sin(π-α)=-
,π<α<
,则tanα=( )
| 12 |
| 13 |
| 3π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知△ABC中,a=
,b=2,B=45°,则角A等于( )
| 6 |
| A、30° | B、90° |
| C、60° | D、60°或120° |
给出下列三个函数的图象:
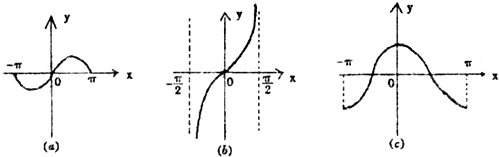
它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )

它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
| f(x)+f(y) |
| 1-f(x)f(y) |
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )
| A、(a)-①,(b)-②,(c)-③ |
| B、(b)-①,(c)-②,(a)-③ |
| C、(c)-①,(b)-②,(a)-③ |
| D、(a)-①,(c)-②,(b)-③ |
若正数a,b满足
+
=1,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| 4 |
| a-1 |
| 16 |
| b-1 |
| A、16 | B、25 | C、36 | D、49 |
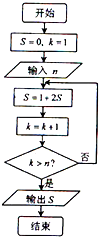 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )