题目内容
17.已知约束条件$\left\{\begin{array}{l}x+y-3≥0\\ x-2y+3≥0\\ x≤a\end{array}\right.$,表示的可行域为D,其中a>1,点(x0,y0)∈D,点(m,n)∈D若3x0-y0与$\frac{n+1}{m}$的最小值相等,则实数a等于2.分析 作出不等式组对应的平面区域,利用z的几何意义即可得到结论.
解答 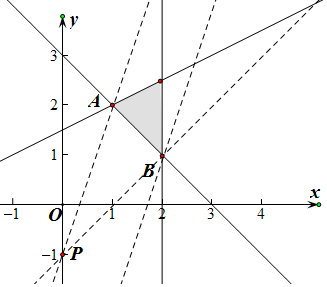 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,
设z1=$\frac{y+1}{x}$=$\frac{n+1}{m}$,
将z1的值转化可行域内的Q点与点P(0,-1)连线的斜率的值,
当Q点在可行域内的B(a,3-a)时,斜率最小,最小值为$\frac{3-a+1}{a}$=$\frac{4-a}{a}$,
设z2=3x-y,
当z2=3x-y过点A(1,2)时3x0-y0的值最小,最小值为3×1-2=1,
∵3x0-y0与$\frac{n+1}{m}$的最小值相等,
∴$\frac{4-a}{a}$=1,
解得a=2,
故答案为:2
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
相关题目
7.设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
8.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1(a>0)的长轴长为4,则C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
5.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数图象的一个对称中心为( )
| A. | $(\frac{7π}{12},0)$ | B. | $(\frac{π}{6},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{2π}{3},-3)$ |
2.下列命题中正确的是( )
| A. | 两条直线都和同一个平面平行,则这两条直线平行 | |
| B. | 两条直线没有公共点,则这两条直线平行 | |
| C. | 两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 一条直线和一个平面内所有直线没有公共点,则这条直线和这个平面平行 |
19.设命题 p:?n∈N,3n≥n2+1,则¬p为( )
| A. | ?n∈N,3n<n2+1 | B. | $?{n_0}∈N,{3^{n_0}}<n_0^2+1$ | ||
| C. | ?n∈N,3n≤n2+1 | D. | $?{n_0}∈N,{3^{n_0}}≥n_0^2+1$ |
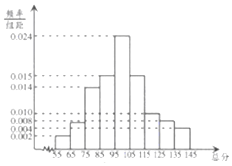 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.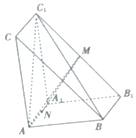 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点