题目内容
16.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )| A. | (-2,0] | B. | (0,2] | C. | (-∞,4] | D. | [4,+∞) |
分析 求出f(x),g(x)的值域,则f(x)的值域为g(x)的值域的子集.
解答 解:f(x)=-|x|≤0,∴f(x)的值域是(-∞,0].设g(x)的值域为A,
∵对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),
∴(-∞,0]⊆A.
设y=ax2-4x+1的值域为B,
则(0,1]⊆B.
由题意当a=0时,上式成立.
当a>0时,△=16-4a≥0,解得0<a≤4.
当a<0时,ymax=$\frac{4a-16}{4a}$≥1,即1-$\frac{4}{a}$≥1恒成立.
综上,a≤4.
故选:C.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
相关题目
7.设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
11.若集合A={0,1,2,4},B={1,2,3},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,1} | C. | {0,1,4} | D. | {1,2} |
8.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1(a>0)的长轴长为4,则C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
5.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数图象的一个对称中心为( )
| A. | $(\frac{7π}{12},0)$ | B. | $(\frac{π}{6},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{2π}{3},-3)$ |
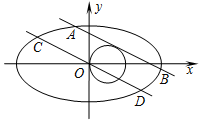 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.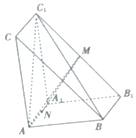 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点