题目内容
求多项式﹙x-1﹚-﹙x-1﹚2+﹙x-1﹚3-﹙x-1﹚4+﹙x-1﹚5的展开式中的x3的系数．
考点：二项式系数的性质
专题：计算题,二项式定理
分析：分别求出﹙x-1﹚3、﹙x-1﹚4、﹙x-1﹚5的x3的系数，即可得出结论．
解答：
解：﹙x-1﹚-﹙x-1﹚2+﹙x-1﹚3-﹙x-1﹚4+﹙x-1﹚5中﹙x-1﹚3、﹙x-1﹚4、﹙x-1﹚5的x3的系数分别为
(-1)3=-1，
(-1)3=-4，
(-1)3=-10，
∴多项式﹙x-1﹚-﹙x-1﹚2+﹙x-1﹚3-﹙x-1﹚4+﹙x-1﹚5的展开式中的x3的系数为-1+4-10=-7．
| C | 3 3 |
| C | 3 4 |
| C | 3 5 |
∴多项式﹙x-1﹚-﹙x-1﹚2+﹙x-1﹚3-﹙x-1﹚4+﹙x-1﹚5的展开式中的x3的系数为-1+4-10=-7．
点评：本题考查二项式系数的性质，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
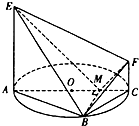如图，AC是圆O的直径，点B在圆O上，∠BAC=30°，BM⊥AC交AC于点M，EA⊥平面ABC，FC∥EA，AC=4，EA=3，FC=1．
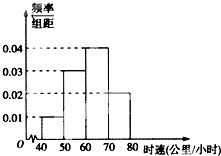已知某一段公路限速60公里/小时，现抽取200辆通过这一段公路的汽车的时速，其频率分布直方图如图所示，则这200辆汽车中在该路段没有超速的有