题目内容
已知△ABC的三个内角A、B、C的对边分别为a、b、c,且a2=
bc.
(1)求cosA的最小值;
(2)若cos(B-C)+cosA=1,求角A.
| 1 |
| 2 |
(1)求cosA的最小值;
(2)若cos(B-C)+cosA=1,求角A.
考点:余弦定理,两角和与差的余弦函数
专题:解三角形
分析:(1)利用余弦定理表示出cosA,进而把a2=
bc代入,利用基本不等式求得其最小值.
(2)利用两角和与差的余弦函数对已知等式恒等变换整理可求得sinBsinC的值,利用已知和正弦定理求得sin2A的值,则A可求.
| 1 |
| 2 |
(2)利用两角和与差的余弦函数对已知等式恒等变换整理可求得sinBsinC的值,利用已知和正弦定理求得sin2A的值,则A可求.
解答:
解:(1)cosA=
=
=
-
≥1-
=
,当且仅当b=c时取等号.
∴cosA的最小值为
.
(2)cos(B-C)+cosA=cos(B-C)-cos(B+C)=cosBcosC+sinBsinC-cosBcosC+sinBsinC=2sinBsinC=1,
∵a2=
bc,
∴2sin2A=sinBsinC,
∴4sin2A=1,
∵0<A<π,
∴sinA=
∴A=
或
.
| b2+c2-a2 |
| 2bc |
b2+c2-
| ||
| 2bc |
| b2+c2 |
| 2bc |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
∴cosA的最小值为
| 3 |
| 4 |
(2)cos(B-C)+cosA=cos(B-C)-cos(B+C)=cosBcosC+sinBsinC-cosBcosC+sinBsinC=2sinBsinC=1,
∵a2=
| 1 |
| 2 |
∴2sin2A=sinBsinC,
∴4sin2A=1,
∵0<A<π,
∴sinA=
| 1 |
| 2 |
∴A=
| π |
| 6 |
| 5π |
| 6 |
点评:本题主要考查了正弦定理和余弦定理的应用,基本不等式的性质.考查了学生基础知识的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
阅读如图给出的程序框图,运行相应的程序,输出的结果S为( )


| A、-1007 | B、1007 |
| C、1008 | D、-3022 |
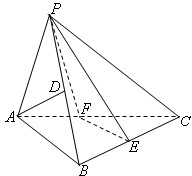 在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.
在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.