��Ŀ����
3��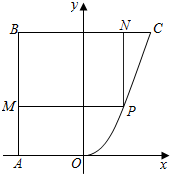 ij������ͼ��ʾ��һ�鲻����ķ�ũҵ�õ�ABCO����AB��BC��OA��BC��AB=BC=4km��AO=2km�����߶�OC����OΪ���㣬�������ϣ��ҶԳ���ƽ����AB�������ߵ�һ�Σ���������Ϊ�Ƽ����У������õع滮����һ�����θ߿Ƽ���ҵ��PMBN�����ε���������BM��BN�ֱ�����AB��BC�ϣ�����P�����߶�OC�ϣ���Ӧ��ι滮����ʹ���������õ���������������õ��������ȷ��0.1 km2����
ij������ͼ��ʾ��һ�鲻����ķ�ũҵ�õ�ABCO����AB��BC��OA��BC��AB=BC=4km��AO=2km�����߶�OC����OΪ���㣬�������ϣ��ҶԳ���ƽ����AB�������ߵ�һ�Σ���������Ϊ�Ƽ����У������õع滮����һ�����θ߿Ƽ���ҵ��PMBN�����ε���������BM��BN�ֱ�����AB��BC�ϣ�����P�����߶�OC�ϣ���Ӧ��ι滮����ʹ���������õ���������������õ��������ȷ��0.1 km2����
���� �������OC�ķ��̣����P�����꣬��P�������ʾ�����ε�������������������������ֵ��
��� �⣺��OΪԭ�㣬ֱ��AOΪx�ᣬ����1 kmΪ��λ���Ƚ�����ͼ��ʾ��ƽ��ֱ������ϵ������C��2��4����B��-2��4����
�����߶�OC���������߷���Ϊx2=2py��p��0����
����22=2p��4����2p=1���������߶�OC���������߷���Ϊx2=y��
��P��x��x2����0��x��2������M��-2��x2����N��x��4����MP=x+2��PN=4-x2��
�����PMBN�����S��x��=MP•PN=��x+2����4-x2��=-x3-2x2+4x+8��0��x��2����
$S'=-3{x^2}-4x+4=-3��x+2����{x-\frac{2}{3}}��$����S'=0��$x=\frac{2}{3}$��x=-2���ᣩ��
��$x�ʣ�{0��\;\;\frac{2}{3}}��$ʱ��S'��0���ຯ��S��$��{0��\;\;\frac{2}{3}}��$���ǵ�����������
��$x�ʣ�{\frac{2}{3}��\;\;2}��$ʱ��S'��0���ຯ��S��$��{\frac{2}{3}��\;\;2}��$���ǵ�����������
��$x=\frac{2}{3}$ʱ��S��x��ȡ�����ֵS��$\frac{3}{2}$��=$\frac{256}{27}$��9.5��
��ѡȡP���AB����ԼΪ2.7 kmʱ����ʹ���������õ�������������ԼΪ9.5 km2��
���� ���⿼���˵����뺯���ĵ����ԣ�������ֵ֮��Ĺ�ϵ��������ε���������ǽ���ؼ���

| A�� | 2 | B�� | 0 | C�� | -1 | D�� | -2 |
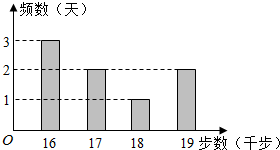 С��Ϊ�˶������壬ÿ���֡������ߡ������üƲ�������ͳ�ƣ�С�����8�조�����ߡ�������Ƶ���ֲ�ֱ��ͼ����ͼ������Ӧ�������������ݱ����������
С��Ϊ�˶������壬ÿ���֡������ߡ������üƲ�������ͳ�ƣ�С�����8�조�����ߡ�������Ƶ���ֲ�ֱ��ͼ����ͼ������Ӧ�������������ݱ����������| �����߲�����ǧ���� | 16 | 17 | 18 | 19 |
| ������������·� | 400 | 440 | 480 | 520 |
���Ӳ���Ϊ16ǧ����17ǧ����18ǧ���ļ�������ѡ2�죬��С����2��ͨ�����������ĵġ������͡�ΪX����X�ķֲ��У�
| A�� | ��-�ޣ�0�� | B�� | $��{-�ޣ�\frac{1}{2a}}��$ | C�� | $��{0��\frac{1}{a}}��$ | D�� | $��{\frac{1}{a}��+��}��$ |