题目内容
12.已知函数f(x)=$\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}$+1(a∈R),f(ln(log25))=5,则f(ln(log52))=( )| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
分析 根据题意,对函数f(x)变形可得$f(x)=\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}+1=\frac{2x+asinx}{{{x^2}+1}}+2$;令$g(x)=f(x)-2=\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}$,分析可得g(x)为奇函数,又由ln(log52)=-ln(log25),结合函数奇偶性的性质即可得答案.
解答 解:根据题意,$f(x)=\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}+1=\frac{2x+asinx}{{{x^2}+1}}+2$;
令$g(x)=f(x)-2=\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}$,则g(x)为奇函数,
g(ln(log25))=f(ln(log25))-2=3,g(ln(log52))=g(-ln(log25))=-3,
f(ln(log52))=g(ln(log52))+2=-3+2=-1,
即f(ln(log52))=-1;
故选:B.
点评 本题考查函数奇偶性的性质,涉及对数的运算性质,关键是构造函数g(x)=f(x)-2,并分析g(x)的奇偶性.

练习册系列答案
相关题目
17.复数$\frac{1}{2+i}$的虚部是( )
| A. | -$\frac{1}{5}$ | B. | -$\frac{1}{5}$i | C. | $\frac{1}{5}$ | D. | $\frac{1}{5}$i |
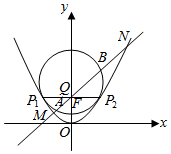 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.