题目内容
1.f(x)是定义在R上的偶函数,其图象关于直线x=2对称,当x∈[-2,2]时,f(x)=-x2+3,则f(-3)=2.分析 由f(x)是定义在R上的偶函数,其图象关于直线x=2对称,推理出f(x)是周期函数,且周期为4,从而f(-3)=f(1),由此能求出结果.
解答 解:∵f(x)是定义在R上的偶函数,∴f(-x)=f(x),
∵其图象关于直线x=2对称,∴f(4-x)=f(x),
∴f(4-x)=f(-x),
∴f(x)是周期函数,且周期为4,
∴f(-3)=f(1)=-12+3=2.
故答案为:2.
点评 本题考查实数值的求法,涉及到函数的周期性、对称性等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想,是基础题.

练习册系列答案
相关题目
11. 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )| A. | 100πcm3 | B. | $\frac{500π}{3}c{m^3}$ | C. | 400πcm3 | D. | $\frac{4000π}{3}c{m^3}$ |
12.已知函数f(x)=$\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}$+1(a∈R),f(ln(log25))=5,则f(ln(log52))=( )
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
9.复数z=$\frac{-4+i}{-i}$的共轭复数是( )
| A. | -1+4i | B. | -1-4i | C. | 1+4i | D. | 1-4i |
6.设集合A={x|-a<x<a},其中a>0,命题p:1∈A,命题q:2∈A,若p∨q为真命题,p∧q为假命题,则a的取值范围是( )
| A. | 0<a<1或a>2 | B. | 0<a<1或a≥2 | C. | 1<a≤2 | D. | 1≤a≤2 |
13.设复数z=1-i,则$\frac{-3+4i}{z+1}$=( )
| A. | -2+i | B. | 2+i | C. | -1+2i | D. | 1+2i |
11.在正项等比数列{an}中,a1008a1010=$\frac{1}{100}$,则lga1+lga2+…+lga2017=( )
| A. | -2016 | B. | -2017 | C. | 2016 | D. | 2017 |
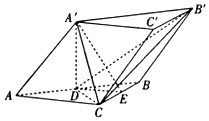 在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.
在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.