题目内容
7.定义域为R的函数f(x)满足f(x+3)=2f(x),当x∈[-1,2)时,f(x)=$\left\{{\begin{array}{l}{{x^2}+x,x∈[-1,0)}\\{-{{(\frac{1}{2})}^{|x-1|}},x∈[0,2)}\end{array}}$.若存在x∈[-4,-1),使得不等式t2-3t≥4f(x)成立,则实数t的取值范围是(-∞,1]∪[2,+∞).
分析 运用二次函数的最值求法和指数函数的单调性,讨论分段函数的两段的最小值,再由f(x)=$\frac{1}{2}$f(x+3),由图象左右平移可知,函数的最值不变,可得x∈[-4,-1),f(x)的最小值为-$\frac{1}{2}$,由题意可得t2-3t≥-2,解不等式即可得到所求t的范围.
解答 解:当x∈[-1,2)时,f(x)=$\left\{{\begin{array}{l}{{x^2}+x,x∈[-1,0)}\\{-{{(\frac{1}{2})}^{|x-1|}},x∈[0,2)}\end{array}}$.
当x∈[-1,0)时,f(x)=(x+$\frac{1}{2}$)2-$\frac{1}{4}$,仅有x=-$\frac{1}{2}$时,取得最小值-$\frac{1}{4}$;
当x∈[0,2)时,f(x)=-($\frac{1}{2}$)|x-1|∈[-1,-$\frac{1}{2}$],
可得x=1时,取得最小值-1;
则当x∈[-1,2)时,f(x)的最小值为-1.
当x∈[-4,-1),x+3∈[-1,2),
由f(x+3)=2f(x),可得
f(x)=$\frac{1}{2}$f(x+3),由图象左右平移可知,函数的最值不变,
可得此时f(x)的最小值为-$\frac{1}{2}$,
由存在x∈[-4,-1),使得不等式t2-3t≥4f(x)成立,
可得t2-3t≥4f(x)的最小值,即为t2-3t≥-2,
解得t≥2或t≤1,
故答案为:(-∞,1]∪[2,+∞).
点评 本题考查不等式的存在性问题的解法,注意运用转化思想,考查分段函数的最值的求法,注意运用二次函数和指数函数的性质,考查化简整理的运算能力,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
17.已知f(x)=$\frac{a}{2}$-$\frac{3}{{2}^{x}+1}$是R上的奇函数,则f(a)的值为( )
| A. | $\frac{7}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
15.已知${(1+x)^{10}}={a_0}+{a_1}(1-x)+{a_2}{(1-x)^2}+…+{a_{10}}{(1-x)^{10}}$,则a0+a8=( )
| A. | 664 | B. | 844 | C. | 968 | D. | 1204 |
12.已知函数f(x)=$\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}$+1(a∈R),f(ln(log25))=5,则f(ln(log52))=( )
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
19.已知双曲线与椭圆x2+$\frac{{y}^{2}}{2}$=1有公共焦点,且双曲线的离心率为$\sqrt{5}$,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{2\sqrt{5}}{5}$ | C. | y=±$\frac{\sqrt{5}}{2}$x | D. | y=±$\frac{1}{2}$x |
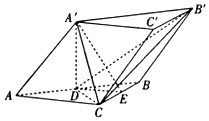 在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.
在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且C1E⊥平面BDE.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且C1E⊥平面BDE.