题目内容
2.已知函数f(x)=x3-ax2+3x+6(Ⅰ)若f(x)在[-$\frac{1}{3}$,+∞)上是增函数,求实数a的取值范围;
(Ⅱ)若x=3是f(x)的一个极值点,求f(x)在[0,a]上的最值.
分析 (Ⅰ)求出导函数,利用$f'(x)在[-\frac{1}{3},+∞]$上恒有f'(x)≥0,转化为$3{x^2}-2ax+3≥0在[-\frac{1}{3},+∞)$上恒成立,①△≤0,②$\left\{\begin{array}{l}△>0\\ \frac{a}{3}<-\frac{1}{3}\\ f'(-\frac{1}{3})≥0\end{array}\right.$,求解即可.
(Ⅱ)依题意,f'(3)=0,求出a,然后求解极值点,判断导函数的符号,然后求解最值.
解答 解:(Ⅰ)f'(x)=3x2-2ax+3∵$f(x)在[-\frac{1}{3},+∞]$上是增函数,
∴$f'(x)在[-\frac{1}{3},+∞]$上恒有f'(x)≥0,
即$3{x^2}-2ax+3≥0在[-\frac{1}{3},+∞)$上恒成立…(2分)
则有
①△≤0,解得-3≤a≤3…(4分)
②$\left\{\begin{array}{l}△>0\\ \frac{a}{3}<-\frac{1}{3}\\ f'(-\frac{1}{3})≥0\end{array}\right.$
解得-5≤a<-3
综上-5≤a≤3…(6分)
(Ⅱ)依题意,f'(3)=0,
即3•9-6a+3=0∴a=5,∴f(x)=x3-5x2+3x+6…(8分)
令f'(x)=3x2-10x-3=0.
得${x_1}=\frac{1}{3},{x_2}=3$,则
当x变化时,f'(x),f(x)的变化情况如下表:
| x | 0 | (0,$\frac{1}{3}$) | $\frac{1}{3}$ | ($\frac{1}{3}$,3) | 3 | (3,5) | 5 |
| f'(x) | + | 0 | - | 0 | + | ||
| f(x) | 6 | ↗ | $6\frac{13}{27}$ | ↘ | -3 | ↗ | 21 |
∴f(x)在[0,5]上的最大值是f(5)=21,最小值是f(3)=-3.…(12分)
点评 本题考查函数的最值的求法,函数的极值以及函数的单调性的判断,考查转化思想以及计算能力.

练习册系列答案
相关题目
12.已知函数f(x)=$\frac{{{{(x+1)}^2}+asinx}}{{{x^2}+1}}$+1(a∈R),f(ln(log25))=5,则f(ln(log52))=( )
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
13.设复数z=1-i,则$\frac{-3+4i}{z+1}$=( )
| A. | -2+i | B. | 2+i | C. | -1+2i | D. | 1+2i |
17. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且C1E⊥平面BDE.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且C1E⊥平面BDE.
(I)求直线BD1与平面BDE所成角的正弦值;
(II)求二面角C-BE-D的余弦值.
 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且C1E⊥平面BDE.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且C1E⊥平面BDE.(I)求直线BD1与平面BDE所成角的正弦值;
(II)求二面角C-BE-D的余弦值.
11.在正项等比数列{an}中,a1008a1010=$\frac{1}{100}$,则lga1+lga2+…+lga2017=( )
| A. | -2016 | B. | -2017 | C. | 2016 | D. | 2017 |
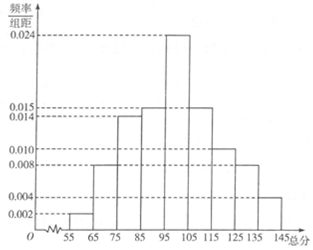 某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.
某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.