题目内容
若{an}是等差数列,则下列数列中仍为等差数列的有( )
(1){an+3};(2){an2};(3){an+1-an};(4){2an};(5){2an+n}.
(1){an+3};(2){an2};(3){an+1-an};(4){2an};(5){2an+n}.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:等差关系的确定
专题:等差数列与等比数列
分析:利用等差数列的定义,对于各个选项中的数列,只要证明第n+1项与第n项的差是常数即可.
解答:
解:设等差数列{an}的公差为d,n≥2时,an-an-1=d,
(1)an+1+3-(an+3)=an+1-an=d为常数,因此{an+3}是等差数列;
(2)an+12-an2=(an+1+an)(an+1-an)=d[2a1+(2n-1)d]不为常数,因此{an2}不是等差数列;
(3)(an+2-an+1)-(an+1-an)=an+2-an=2d为常数,因此{an+1-an}是等差数列;
(4)2an+1-2an=2(an+1-an)=2d是常数,因此{2an}是等差数列;
(5)2an+1+(n+1)-(2an+n)=2(an+1-an)+1=2d+1是常数,因此{2an+n}是等差数列;
综上可知:只有(1)、(3)、(4)、(5)是等差数列,故4个,
故选:D.
(1)an+1+3-(an+3)=an+1-an=d为常数,因此{an+3}是等差数列;
(2)an+12-an2=(an+1+an)(an+1-an)=d[2a1+(2n-1)d]不为常数,因此{an2}不是等差数列;
(3)(an+2-an+1)-(an+1-an)=an+2-an=2d为常数,因此{an+1-an}是等差数列;
(4)2an+1-2an=2(an+1-an)=2d是常数,因此{2an}是等差数列;
(5)2an+1+(n+1)-(2an+n)=2(an+1-an)+1=2d+1是常数,因此{2an+n}是等差数列;
综上可知:只有(1)、(3)、(4)、(5)是等差数列,故4个,
故选:D.
点评:本题考查了等差数列的证明,正确运用等差数列的定义是关键.

练习册系列答案
相关题目
函数f(x)=
的定义域为( )
| ||||
| x |
| A、[-4,1] |
| B、[-4,0) |
| C、(0,1] |
| D、[-4,0)∪(0,1] |
已知sin(30°+α)=
,则cos(60°-α)的值为( )
| ||
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
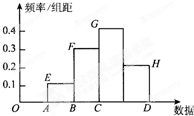 如图,已知样本容量为100,在样本频率分布直方图中,各小长方形的高的比是AE:BF:CG:DH=1:3:4:2,那么第3小组的频率与频数分别为( )
如图,已知样本容量为100,在样本频率分布直方图中,各小长方形的高的比是AE:BF:CG:DH=1:3:4:2,那么第3小组的频率与频数分别为( )| A、0.4,40 |
| B、0.3,30 |
| C、0.2,20 |
| D、0.1,10 |
已知A(7,8),B(3,5),则向量
方向上的单位向量的坐标是( )
| BA |
A、(-
| ||||
B、(
| ||||
C、(
| ||||
| D、(4,3) |
若复数z=
(b∈R,i是虚数单位)是纯虚数,则复数z是( )
| 1+bi |
| 2+i |
A、
| ||
B、-
| ||
| C、-i | ||
| D、i |
下列命题正确的是( )
| A、单位向量都相等 | ||||||||||||
B、若
| ||||||||||||
C、|
| ||||||||||||
D、若
|
函数y=
cos2x-
sin2x+2的单调递减区间为( )
| ||
| 5 |
| 3 |
| 5 |
A、[-
| ||||
B、[
| ||||
C、[-
| ||||
D、[
|