题目内容
函数f(x)=
的定义域为( )
| ||||
| x |
| A、[-4,1] |
| B、[-4,0) |
| C、(0,1] |
| D、[-4,0)∪(0,1] |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数f(x)的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答:
解:∵函数f(x)=
,
∴
;
解得-4≤x≤1,且x≠0,
∴f(x)的定义域为[-4,0)∪(0,1].
故答案为:D.
| ||||
| x |
∴
|
解得-4≤x≤1,且x≠0,
∴f(x)的定义域为[-4,0)∪(0,1].
故答案为:D.
点评:本题考查了求函数定义域的问题,解题的关键是列出使函数有意义的关于自变量的不等式组,是基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
已知a,b,a+b成等差数列,a,b,ab成等比数列,且logc(ab)>1,则c的取值范围是( )
| A、0<c<1 |
| B、1<c<8 |
| C、c>8 |
| D、0<c<1或c>8 |
已知点P(x,y)满足
,则
的最大值为( )
|
| y |
| x+1 |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
下列说法正确的是( )
| A、甲乙两个班期末考试数学平均成绩相同,这表明这两个班数学学习情况一样 |
| B、期末考试数学成绩的方差甲班比乙班的小,这表明甲班的数学学习情况比乙班好 |
| C、期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班大,则数学学习甲班比乙班好 |
| D、期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班小,则数学学习甲班比乙班好 |
一个凸多边形的内角成等差数列,其中最小的内角为
,公差为
,则这个多边形的边数为( )
| 2π |
| 3 |
| π |
| 36 |
| A、8 | B、9 | C、16 | D、9或16 |
已知一个正四面体和一个正八面体的棱长相等,把它们拼接起来,使一个表面重合,所得多面体的面数有( )
| A、7 | B、8 | C、9 | D、10 |
向面积为S的△ABC内任投一点P,则△PBC的面积小于
的概率为( )
| S |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
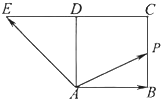 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中