题目内容
函数y=-
sin2x+cos2x,x∈[
,
]的值域为 .
| 3 |
| π |
| 6 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:首先通过恒等变换把函数关系式变形成正弦型函数,然后根据定义域求函数的值域.
解答:
解:函数y=-
sin2x+cos2x=-2sin(2x-
)
∵x∈[
,
]
∴
≤2x-
≤
∴
≤sin(2x-
)≤1
∴-2≤-2sin(2x-
)≤-1
即:函数的值域为:[-2,-1]
故答案为:[-2,-1]
| 3 |
| π |
| 6 |
∵x∈[
| π |
| 6 |
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴-2≤-2sin(2x-
| π |
| 6 |
即:函数的值域为:[-2,-1]
故答案为:[-2,-1]
点评:本题考查的知识点:三角函数的恒等变形,正弦型三角函数的定义域和值域

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
数列{an}是等差数列,若
<-1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
| a11 |
| a10 |
| A、11 | B、17 | C、19 | D、21 |
已知a,b,a+b成等差数列,a,b,ab成等比数列,且logc(ab)>1,则c的取值范围是( )
| A、0<c<1 |
| B、1<c<8 |
| C、c>8 |
| D、0<c<1或c>8 |
已知点P(x,y)满足
,则
的最大值为( )
|
| y |
| x+1 |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
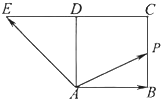 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中