题目内容
14．若实数x，y满足$\left\{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}\right.$，则z=2x-y的最小值为（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}\right.$作出可行域如图，
化目标函数z=2x-y为y=2x-z，
由图可知，当直线y=2x-z过时A（0，1）时，z有最小值为：-1
故选：B．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
计算高手系列答案
相关题目
4．方程$a=sin（2x+\frac{π}{3}），x∈[0，\frac{π}{2}]$上有解，则实数a的取值范围（ ）
| A． | [-1，1] | B． | $[-\frac{{\sqrt{3}}}{2}，\frac{{\sqrt{3}}}{2}]$ | C． | $[-\frac{{\sqrt{3}}}{2}，1]$ | D． | [0，1] |
5．“a=1”是“函数f（x）=a|x|+b，b∈R在区间[0，+∞）上为增函数”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
9．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜2π）在一个周期内的部分对应值如下表：
（Ⅰ）求f（x）的解析式；
（Ⅱ）求函数g（x）=f（x）+2sinx的最大值和最小值．
| x | $-\frac{π}{2}$ | 0 | $\frac{π}{6}$ | $\frac{π}{2}$ |
| f（x） | -1 | 1 | $\frac{1}{2}$ | -1 |
（Ⅱ）求函数g（x）=f（x）+2sinx的最大值和最小值．
3．某同学在用描点法画二次函数y=ax2+bx+c的图象时，列出下面的表格：
由于粗心，他算错了其中一个y值，则这个错误的数值时（ ）
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
| A． | -11 | B． | -2 | C． | 1 | D． | -5 |
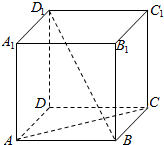已知正方体ABCD-A1B1C1D1的棱长是a，用向量法证明AC⊥BD1．