题目内容
2．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，x）．若$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$平行，则实数x的值是（ ）| A． | 4 | B． | -1 | C． | -4 |
分析 利用向量坐标运算、向量共线定理即可得出．
解答 解：$\overrightarrow{a}$+$\overrightarrow{b}$=（-1，2+x）．
$\overrightarrow{a}$-$\overrightarrow{b}$=（3，2-x），
∵$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$平行，
∴3（2+x）+（2-x）=0，
解得x=-4．
故选：C．
点评 本题考查了向量坐标运算、向量共线定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
12．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，${\overline{x}}_{1}$，${\overline{x}}_{2}$分别表示甲、乙两名运动员这项测试成绩的平均数，s${\;}_{1}^{2}$，s${\;}_{2}^{2}$分别表示甲、乙两名运动员这项测试成绩的方差，则有（ ）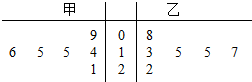
| A． | ${\overline{x}}_{1}$＞${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ | B． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＞${s}_{2}^{2}$ | ||
| C． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ |
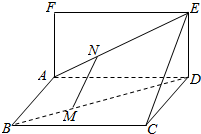如图，已知矩形ABCD和矩形ADEF所在平面互相垂直，点M，N分别在对角线BD、AE上，且BM=$\frac{1}{3}$BD，AN=$\frac{1}{3}$AE，求证：MN∥平面CDE．