题目内容
5．“a=1”是“函数f（x）=a|x|+b，b∈R在区间[0，+∞）上为增函数”的（ ）| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
分析 当x≥0时，f（x）=a|x|+b=ax+b，当a＞0时，函数f（x）单调递增．即可判断出．
解答 解：当x≥0时，f（x）=a|x|+b=ax+b，当a＞0时，函数f（x）单调递增．
∴“a=1”是“函数f（x）=a|x|+b，b∈R在区间[0，+∞）上为增函数”的充分不必要条件．
故选：A．
点评 本题考查了函数的单调性、简易逻辑的判定方法，考查了推理能力，属于中档题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
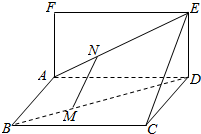如图，已知矩形ABCD和矩形ADEF所在平面互相垂直，点M，N分别在对角线BD、AE上，且BM=$\frac{1}{3}$BD，AN=$\frac{1}{3}$AE，求证：MN∥平面CDE．