题目内容
 如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2
如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2| 3 |
考点:与圆有关的比例线段
专题:直线与圆,立体几何
分析:连结OA,由切割线定理得PA2=PB•PC,解得PB=2,所以BC=4,PO=4,OA=2,∠PAO=90°,由此得到∠P=30°,∠POA=60°,从而能求出∠PCA=30°.
解答:
解:连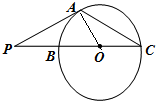 结OA,
结OA,
∵P是圆O外的一点,PA为切线,A为切点,
割线PBC经过圆心O,PC=6,PA=2
,
∴PA2=PB•PC,
∴(2
)2=6PB,解得PB=2,
∴BC=4,PO=4,OA=2,∠PAO=90°,
∴∠P=30°,∴∠POA=60°,
∴∠PCA=30°.
故答案为:30°.
 结OA,
结OA,∵P是圆O外的一点,PA为切线,A为切点,
割线PBC经过圆心O,PC=6,PA=2
| 3 |
∴PA2=PB•PC,
∴(2
| 3 |
∴BC=4,PO=4,OA=2,∠PAO=90°,
∴∠P=30°,∴∠POA=60°,
∴∠PCA=30°.
故答案为:30°.
点评:本题考查与圆有关的角的求法,考查切割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
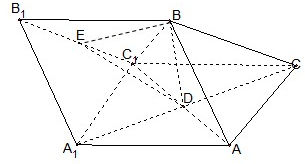 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.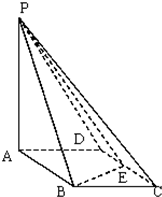 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.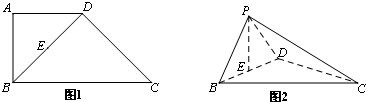
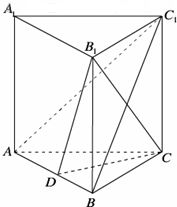 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,