题目内容
如图1,在直角梯形ABCD中,已知AD∥BC,AD=AB=1,∠BAD=90°,∠BCD=45°,E为对角线BD中点.现将△ABD沿BD折起到△PBD的位置,使平面PBD⊥平面BCD,如图2.
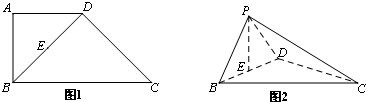
(Ⅰ)若点F为BC中点,证明:EF∥平面PCD;
(Ⅱ)证明:平面PBC⊥平面PCD.

(Ⅰ)若点F为BC中点,证明:EF∥平面PCD;
(Ⅱ)证明:平面PBC⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)由三角形中位线定理得EF∥CD,由此能证明EF∥平面PCD.
(Ⅱ) 由已知条件推导出平面PBD⊥平面BCD,由此得到CD⊥PB,从而推导出PB⊥平面PCD,由此能证明平面PBC⊥平面PCD.
(Ⅱ) 由已知条件推导出平面PBD⊥平面BCD,由此得到CD⊥PB,从而推导出PB⊥平面PCD,由此能证明平面PBC⊥平面PCD.
解答:
解:(Ⅰ)在△BCD中,点E、F分别为BD、BC的中点,
∴EF∥CD…(2分)
又EF?平面PCDCD?平面PCD
∴EF∥平面PCD.…(4分)
(Ⅱ) 在直角梯形ABCD中,
∵AD∥BC,AD=AB=1,∠BAD=90°,∠BCD=45°,
∴CD⊥BD,…(6分)
∵平面PBD⊥平面BCD,
且平面PBD∩平面BCD=BD,CD?平面BCD,
∴CD⊥平面PBD…(7分)
∴CD⊥PB…(9分)
∵PB⊥PD PD∩CD=D
∴PB⊥平面PCD…(10分)
又PB?平面PBC
∴平面PBC⊥平面PCD.…(12分)
∴EF∥CD…(2分)
又EF?平面PCDCD?平面PCD
∴EF∥平面PCD.…(4分)
(Ⅱ) 在直角梯形ABCD中,
∵AD∥BC,AD=AB=1,∠BAD=90°,∠BCD=45°,
∴CD⊥BD,…(6分)
∵平面PBD⊥平面BCD,
且平面PBD∩平面BCD=BD,CD?平面BCD,
∴CD⊥平面PBD…(7分)
∴CD⊥PB…(9分)
∵PB⊥PD PD∩CD=D
∴PB⊥平面PCD…(10分)
又PB?平面PBC
∴平面PBC⊥平面PCD.…(12分)
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2
如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2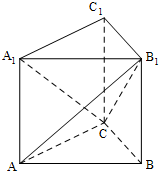 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB=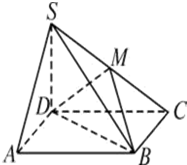 如图四棱锥S-ABCD,底面ABCD是正方形,SD⊥底面ABCD,M为SC的中点.
如图四棱锥S-ABCD,底面ABCD是正方形,SD⊥底面ABCD,M为SC的中点.