题目内容
11.等差数列{an}中,a1=13,a4=1,则公差d=-4.分析 由题目给出的已知条件,直接代入等差数列的通项公式求公差即可.
解答 解:在等差数列{an}中,
由a1=13,a4=1,得d=$\frac{{a}_{4}-{a}_{1}}{4-1}$=$\frac{1-13}{3}=-4$.
∴等差数列{an}的公差d=-4.
故答案为:-4.
点评 本题考查了等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
相关题目
2.下列函数中是奇函数,且最小正周期是π的函数是( )
| A. | $y=cos({\frac{3π}{2}-2x})$ | B. | y=|cosx| | C. | $y=sin({\frac{π}{2}+2x})$ | D. | y=|sinx| |
19.已知直线l1:ax+2y=0与直线l2:x+(a-1)y+a2-1=0平行,则实数a的值是( )
| A. | -1或2 | B. | 0或1 | C. | -1 | D. | 2 |
20.已知一个几何体的三视图如图所示,则该几何体的表面积为( )
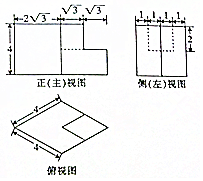

| A. | 64+18$\sqrt{3}$ | B. | 64+16$\sqrt{3}$ | C. | 96 | D. | 92-2$\sqrt{3}$ |