在△ABC中.若a2+b2-c2+ab=0.则C的值是$\frac{2}{3}π$．题目和参考答案——青夏教育精英家教网—

题目内容

16．在△ABC中，若a²+b²-c²+ab=0，则C的值是$\frac{2}{3}π$．

分析利用余弦定理表示出cosC，将已知等式变形后代入求出cosC的值，即可确定出C的度数．

解答解：∵在△ABC中，a²+b²-c²+ab=0，即a²+b²-c²=-ab，
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$，
∵C∈（0，π），
∴C=$\frac{2}{3}π$．
故答案为：$\frac{2}{3}π$．

点评此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．

练习册系列答案

7．已知关于x的不等式|x-a|+|x-3|≥2a的解集为R，则实数a的最大值为1．

4．

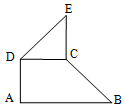如图，直角梯形ABCD中，AB∥CD，AB⊥AD，AB=2CD=2AD=2．在等腰直角三角形CDE中，∠C=90°，点M，N分别为线段BC，CE上的动点，若$\overrightarrow{AM}•\overrightarrow{AN}=\frac{5}{2}$，
则$\overrightarrow{MD}•\overrightarrow{DN}$的取值范围是[$\frac{2\sqrt{2}-5}{2}$，-1]．

11．等差数列{a_n}中，a₁=13，a₄=1，则公差d=-4．

1．公差为2的等差数列{a_n}的前20项中，偶数项和与奇数项和的差为20．

8．（1）计算：8${\;}^{\frac{2}{3}}$+（$\frac{16}{81}$）${\;}^{-\frac{3}{4}}$-（$\sqrt{2}$-1）⁰；
（2）计算：9${\;}^{lo{g}_{9}2}$+$\frac{1}{3}$log₆8-2log${\;}_{{6}^{-1}}$$\sqrt{3}$．

5．若函数f（x）=asinωx+bcosωx（0＜ω＜5，ab≠0）的图象的一条对称轴方程是$x=\frac{π}{4ω}$，函数f'（x）的图象的一个对称中心是$（{\frac{π}{8}，0}）$，则f（x）的最小正周期是（　　）

6．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{3}$，且过点$（{\sqrt{3}，2}）$．
（1）求椭圆C的方程；
（2）过A（a，0）且相互垂直的两条直线l₁，l₂，与椭圆C的另一个交点分别为P，Q，问直线PQ是否经过定点？若是，求出该定点的坐标，否则，说明理由．

试题分类